题目内容
如图所示,AB是⊙O的直径,弦BC=2cm,∠ABC=60º.

(1)求⊙O的直径;
(2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2cm/s的速度从点A出发沿着AB方向运动,同时动点F以1cm/s的速度从点B出发沿BC方向运动,设运动时间为t(s)(0<t<2),连结EF,当t为何值时,△BEF为直角三角形.

(1)求⊙O的直径;
(2)若D是AB延长线上一点,连结CD,当BD长为多少时,CD与⊙O相切;
(3)若动点E以2cm/s的速度从点A出发沿着AB方向运动,同时动点F以1cm/s的速度从点B出发沿BC方向运动,设运动时间为t(s)(0<t<2),连结EF,当t为何值时,△BEF为直角三角形.
(1)4cm;(2)2cm;(3)t=1s或t=1.6s时
试题分析:(1)先根据圆周角定理可得∠ACB=90º,再由∠ABC=60º可得∠BAC=30º,再根据含30°角的直角三角形的性质即可求得结果;
(2)连结OC,根据切线的性质可得∠OCD=90º,根据圆周角定理可得∠COD=60º,从而可得∠D=30º ,再根据含30°角的直角三角形的性质即可求得结果;
(3)根据题意得BE=(4-2t)cm,BF=tcm,分∠EFB=90º与∠FEB=90º两种情况结合相似三角形的性质即可求得结果.
(1)∵AB是⊙O的直径
∴∠ACB=90º
∵∠ABC=60º
∴∠BAC=180º-∠ACB-∠ABC=30º
∴AB=2BC=4cm,即⊙O的直径为4cm;
(2)如图,连结OC.

∵CD切⊙O于点C,
∴CD⊥CO
∴∠OCD=90º
∵∠BAC=30º
∴∠COD=2∠BAC=60º.
∴∠D=180º-∠COD-∠OCD=30º
∴OD=2OC=4cm
∴BD=OD-OB=4-2=2cm
∴当BD长为2cm时,CD与⊙O相切;
(3)根据题意,得BE=(4-2t)cm,BF=tcm;

如图,当∠EFB=90º时,△BEF为直角三角形,
∵∠EFB=∠ACB,∠B=∠B
∴△BEF∽△BAC
∴
 ,即
,即 ,解得t=1.
,解得t=1.
如图,当∠FEB=90º时,△BEF为直角三角形,
∵∠FEB=∠ACB,∠B=∠B,
∴△BEF∽△BCA.
∴
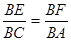 ,即
,即 ,解得t=1.6.
,解得t=1.6. ∴当t=1s或t=1.6s时,△BEF为直角三角形.
点评:本题知识点多,综合性强,难度较大,一般是中考压轴题,主要考查学生对圆的性质的熟练掌握情况.

练习册系列答案
相关题目

 ,求BF的长.
,求BF的长. 半径为3cm,⊙
半径为3cm,⊙ 的半径为7 cm,若⊙
的半径为7 cm,若⊙
 ,求AB的长.
,求AB的长.

 ,tanC=
,tanC=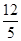 .点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.
.点D为边BC上的动点(点D不与B、C重合),以D为圆心,BD为半径的⊙D交边AB于点E.
 与
与 的函数关系式,并写出函数定域义;
的函数关系式,并写出函数定域义; CF,联结DF.
CF,联结DF.