题目内容
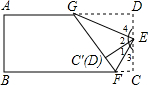
 如图,先找到长方形纸的宽DC的中点E,将∠C过E点折起任意一个角,折痕是EF,再将∠D过E点折起,使DE和CE重合,折痕是GE,请探索下列问题:
如图,先找到长方形纸的宽DC的中点E,将∠C过E点折起任意一个角,折痕是EF,再将∠D过E点折起,使DE和CE重合,折痕是GE,请探索下列问题:(1)∠FEC'和∠GEC′互为余角吗?为什么?
(2)∠GEF是直角吗?为什么?
(3)在上述折纸图形中,还有哪些互为余角?还有哪些互为补角?
分析:(1)根据翻折的性质可得∠3=∠1,∠4=∠2,然后根据平角等于180°求出∠1+∠2=90°;
(2)根据∠GEF=∠1+∠2计算即可得解;
(3)根据互余的两个角的和等于90°,互补的两个角的和等于180°分别找出互余和互补的角即可.
(2)根据∠GEF=∠1+∠2计算即可得解;
(3)根据互余的两个角的和等于90°,互补的两个角的和等于180°分别找出互余和互补的角即可.
解答:解:(1)根据折叠得,∠3=∠1,∠4=∠2,
∵∠1+∠2+∠3+∠4=180°,
∴∠1+∠2=90°,
即∠FEC′+∠GEC′=90°,
故∠FEC′和∠GEC′互余;
(2)∵∠GEF=∠1+∠2=90°,
∴∠GEF是直角;
(3)互余的角有:∠3和∠4,∠1和∠EFG,∠2和∠EGF;
互补的角有:∠AGF和∠DFG,∠CEC′和∠DEC′.
∵∠1+∠2+∠3+∠4=180°,
∴∠1+∠2=90°,
即∠FEC′+∠GEC′=90°,
故∠FEC′和∠GEC′互余;
(2)∵∠GEF=∠1+∠2=90°,
∴∠GEF是直角;
(3)互余的角有:∠3和∠4,∠1和∠EFG,∠2和∠EGF;
互补的角有:∠AGF和∠DFG,∠CEC′和∠DEC′.
点评:本题考查了余角和补角,翻折变换的性质,熟练掌握折叠的性质找出相等的角是解题的关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
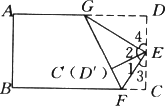

 如图,先找到长方形纸的宽DC的中点E,将∠C过E点折起任意一个角,折痕是EF,再将∠D过E点折起,使DE和CE重合,折痕是GE,请探索下列问题:
如图,先找到长方形纸的宽DC的中点E,将∠C过E点折起任意一个角,折痕是EF,再将∠D过E点折起,使DE和CE重合,折痕是GE,请探索下列问题: