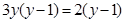题目内容
已知关于x的一元二次方程（a﹣l）x2﹣2x+l=0有两个不相等的实数根，则a的取值范围是【 】
| A．a＞2 | B．a＜2 | C．a＜2且a≠l | D．a＜﹣2 |
C
利用一元二次方程根的判别式列不等式，解不等式求出a的取值范围，结合一元二次方程定义作出判断：
∵由△=4﹣4（a﹣1）=8﹣4a＞0解得：a＜2。
又根据一元二次方程二次顶系数不为0的定义，a﹣1≠0，∴a＜2且a≠1。故选C
∵由△=4﹣4（a﹣1）=8﹣4a＞0解得：a＜2。
又根据一元二次方程二次顶系数不为0的定义，a﹣1≠0，∴a＜2且a≠1。故选C
练习册系列答案
口算题天天练系列答案
相关题目
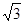≈1.732。结果精确到0.01）
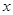的方程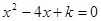
（
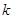为常数）有两个不相等的实数根，那么k _．