题目内容
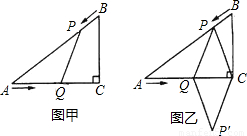
已知,如图①,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,点P从点A沿AB以每秒2cm的速度向点B运动,点Q从点C以每秒1cm的速度向点A运动,设点P、Q分别从点A、C同时出发,运动时间为t(秒)(0<t<6),回答下列问题:
(1)直接写出线段AP、AQ的长(含t的代数式表示):AP=______,AQ=______;
(2)设△APQ 的面积为S,写出S与t的函数关系式;
(3)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时间t,使四边形PQP′C为菱形?若存在,求出此时t的值;若不存在,说明理由.
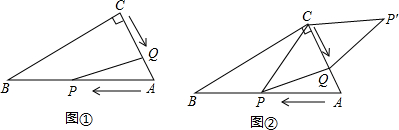
解:(1)∵在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,
∴AC=6,
∴由题意知:AP=2t,AQ=6-t,
(2)如图①过点P作PH⊥AC于H.
∵∠C=90°,∠A=60°,AB=12cm,
∴∠B=30°,
∴∠HPA=30°,
∵AP=2t,AH=t,
∴PH= t,
t,
∴S= ×AQ×PH=
×AQ×PH= ×
× t×(6-t)=-
t×(6-t)=- t2+3
t2+3 t;
t;

(3)当t=4时,四边形PQP′C是菱形,
证明:如图②过点P作PM⊥AC于M,
∵CQ=t,由(2)可知,AM= AP=tcm,
AP=tcm,
∴QC=AM,当PC=PQ时,即CM=MQ=AQ= AC=2时,
AC=2时,
∴四边形PQP′C是菱形,
即当t=4时,四边形PQP′C是菱形.
分析:(1)根据∠A=60°,AB=12cm,得出AC的长,进而得出AP=2t,AQ=6-t.
(2)过点P作PH⊥AC于H.由AP=2t,AH=t,得出PH= t,从而求得S与t的函数关系式;
t,从而求得S与t的函数关系式;
(3)过点P作PM⊥AC于M,根据菱形的性质得PQ=PC,则可得出PN=QM=CM,求得t即可.
点评:此题主要考查了相似三角形的判定和性质、勾股定理、菱形的性质等知识点,是中考压轴题,难度偏大,正确利用菱形判定得出是解题关键.
∴AC=6,
∴由题意知:AP=2t,AQ=6-t,
(2)如图①过点P作PH⊥AC于H.
∵∠C=90°,∠A=60°,AB=12cm,
∴∠B=30°,
∴∠HPA=30°,
∵AP=2t,AH=t,
∴PH=
 t,
t,∴S=
 ×AQ×PH=
×AQ×PH= ×
× t×(6-t)=-
t×(6-t)=- t2+3
t2+3 t;
t; 
(3)当t=4时,四边形PQP′C是菱形,
证明:如图②过点P作PM⊥AC于M,
∵CQ=t,由(2)可知,AM=
 AP=tcm,
AP=tcm,∴QC=AM,当PC=PQ时,即CM=MQ=AQ=
 AC=2时,
AC=2时,∴四边形PQP′C是菱形,
即当t=4时,四边形PQP′C是菱形.
分析:(1)根据∠A=60°,AB=12cm,得出AC的长,进而得出AP=2t,AQ=6-t.
(2)过点P作PH⊥AC于H.由AP=2t,AH=t,得出PH=
 t,从而求得S与t的函数关系式;
t,从而求得S与t的函数关系式;(3)过点P作PM⊥AC于M,根据菱形的性质得PQ=PC,则可得出PN=QM=CM,求得t即可.
点评:此题主要考查了相似三角形的判定和性质、勾股定理、菱形的性质等知识点,是中考压轴题,难度偏大,正确利用菱形判定得出是解题关键.

练习册系列答案
相关题目

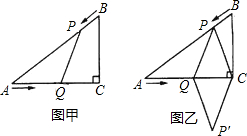


 ),求y与t之间的函数关系式;
),求y与t之间的函数关系式; C,那么是否存在某时刻t,使四边形PQ
C,那么是否存在某时刻t,使四边形PQ