题目内容
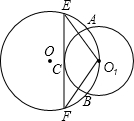 ⊙O与⊙O1相交于A、B,R、r分别为⊙O与⊙O1的半径,且R>r.
⊙O与⊙O1相交于A、B,R、r分别为⊙O与⊙O1的半径,且R>r.(1)C在⊙O1上,且是⊙O1与⊙O相交所得劣弧的中点,过C作⊙O1的切线交⊙O于E、F,求证:O1E•O1F为定值;
(2)如果按前面的条件不变,而是过劣弧ACB上任一点G作⊙O1的切线与⊙O相交(A、B、C三点除外),(1)中的结论仍成立吗?请画出图形,并证明你的结论.
分析:(1)过O1作⊙O直径O1D交⊙O1于C′,连接DE、O1A、O1B、OA、OB,可以证明Rt△O1CE∽Rt△O1ED,然后根据垂径定理即可求证;
(2)作⊙O的直径O1D,连接DE、O1G,可以证明Rt△O1DE∽Rt△O1FG即可求证.
(2)作⊙O的直径O1D,连接DE、O1G,可以证明Rt△O1DE∽Rt△O1FG即可求证.
解答: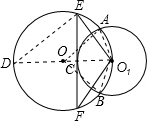
(1)证明:如图(1)过O1作⊙O直径O1D交⊙O1于C′,连接DE、O1A、O1B、OA、OB,
∵OA=OB,O1A=O1B,OO1为公共边,
∴△AOO1≌△BOO1,
∴∠AO1C′=∠BO1C′,
∴弧AC′=弧BC′,
∴C′是弧AB中点,
又∵C是AB中点,
∴C与C′重合,
∵EF是⊙O1的切线,
∴∠O1ED=∠O1CE=90°,
∴△O1CE∽△O1ED,
∴Rt△O1CE∽Rt△O1ED,
∴
=
,即O1E2=O1C•O1D=2Rr(5分)
由垂径定理知O1E=O1F
∴O1E•O1F=2Rr,即O1E•O1F为定值.(6分)
(2)(1)中的结论仍成立.(7分)
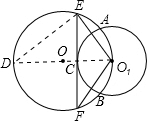
证明:如图(2),作⊙O的直径O1D,连接DE、O1G,(8分)
则∠D=∠F,EF是⊙O1的切线,
∴∠O1ED=∠O1GF=90°,
∴Rt△O1DE∽Rt△O1FG,( 9分)
∴
=
,
∴O1E•O1F=O1D•O1G=2Rr,
即O1E•O1F为定值.(10分)


(1)证明:如图(1)过O1作⊙O直径O1D交⊙O1于C′,连接DE、O1A、O1B、OA、OB,
∵OA=OB,O1A=O1B,OO1为公共边,
∴△AOO1≌△BOO1,
∴∠AO1C′=∠BO1C′,
∴弧AC′=弧BC′,
∴C′是弧AB中点,
又∵C是AB中点,
∴C与C′重合,
∵EF是⊙O1的切线,
∴∠O1ED=∠O1CE=90°,
∴△O1CE∽△O1ED,
∴Rt△O1CE∽Rt△O1ED,
∴
| O1D |
| O1C |
| O1D |
| O1E |
由垂径定理知O1E=O1F
∴O1E•O1F=2Rr,即O1E•O1F为定值.(6分)
(2)(1)中的结论仍成立.(7分)
证明:如图(2),作⊙O的直径O1D,连接DE、O1G,(8分)
则∠D=∠F,EF是⊙O1的切线,
∴∠O1ED=∠O1GF=90°,
∴Rt△O1DE∽Rt△O1FG,( 9分)
∴
| O1F |
| O1D |
| O1G |
| O1E |
∴O1E•O1F=O1D•O1G=2Rr,
即O1E•O1F为定值.(10分)
点评:本题主要考查了相似三角形的判定与性质,证明等积式成立的基本方法是转化为比例式,然后转化为证明三角形相似.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
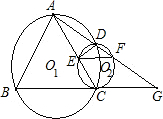 如图,已知等边三角形△ABC内接于⊙O1,⊙O2与BC相切于C,与AC相交于E,与⊙O1相交于另一点D,直线AD交⊙O2于另一点F,交BC的延长线于G,点F为AG的中点.对于如下四个结论:①EF∥BC;②BC=FC;③DE•AG=AB•EC;④弧AD=弧DC.其中一定成立的是( )
如图,已知等边三角形△ABC内接于⊙O1,⊙O2与BC相切于C,与AC相交于E,与⊙O1相交于另一点D,直线AD交⊙O2于另一点F,交BC的延长线于G,点F为AG的中点.对于如下四个结论:①EF∥BC;②BC=FC;③DE•AG=AB•EC;④弧AD=弧DC.其中一定成立的是( )| A、①②④ | B、②③ | C、①③④ | D、①②③④ |
已知⊙O1的半径为3
cm,⊙O2的半径为5cm,与⊙O1相交于点D、E.若两圆的公共弦DE的长是6cm(圆心O1、O2在公共弦DE的两侧),则两圆的圆心距O1O2的长为( )
| 5 |
| A、2cm | B、10cm |
| C、2cm或10cm | D、4cm |
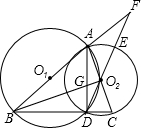 ⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA延长线于F,BO2交AD于G,连接AD.
⊙O1、⊙O2于B、C两点,延长DO2交⊙O2于E,交BA延长线于F,BO2交AD于G,连接AD.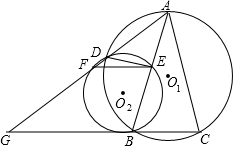 点E,与⊙O1相交于点D,直线AD交⊙O2于点F,交CB的延长线于点G.求证:
点E,与⊙O1相交于点D,直线AD交⊙O2于点F,交CB的延长线于点G.求证: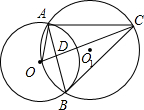 如图,⊙O与⊙O1相交于A、B两点,点O在⊙On上,⊙On的弦OC交AB于点D.
如图,⊙O与⊙O1相交于A、B两点,点O在⊙On上,⊙On的弦OC交AB于点D.