题目内容
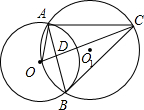如图，⊙O与⊙O1相交于A、B两点，点O在⊙On上，⊙On的弦OC交AB于点D．（1）求证：OA2=OC•OD；
（2）如果AC+BC=
| 3 |
| 3 |
分析：（1）欲证OA2=OC•OD，通过证明△AOC∽△DOA可以得出；
（2）因为AC+BC=
OC，⊙O的半径为r，欲证AB=
r，只需证明（AC+BC）：OC=AB：OA；通过证明△AOC∽△DOA，△OBD∽△OCB，得出比例形式相加，即可得出．
（2）因为AC+BC=
| 3 |
| 3 |
解答：
证明：（1）连接OB．
∵OA=OB，
∴∠OAB=∠OBA．
∵∠OCA=∠OBA，
∴∠OAB=∠OCA．
∵∠AOC=∠DOA，
∴△AOC∽△DOA．
∴
=
，
∴OA2=OC•OD．
（2）∵△AOC∽△DOA，
∴
=
．
同理可得，
=
．
∴
+
=
+
，
即
=
．
∵AC+BC=
OC，OA=r，
∴AB=
r．
证明：（1）连接OB．∵OA=OB，
∴∠OAB=∠OBA．
∵∠OCA=∠OBA，
∴∠OAB=∠OCA．
∵∠AOC=∠DOA，
∴△AOC∽△DOA．
∴
| OA |
| OD |
| OC |
| OA |
∴OA2=OC•OD．
（2）∵△AOC∽△DOA，
∴
| AC |
| OC |
| DA |
| OA |
同理可得，
| BC |
| OC |
| DB |
| OB |
∴
| AC |
| OC |
| BC |
| OC |
| DA |
| OA |
| DB |
| OB |
即
| AC+BC |
| OC |
| AB |
| OA |
∵AC+BC=
| 3 |
∴AB=
| 3 |
点评：本题考查了相似三角形的性质．特别注意：第（2）小题构思巧妙，解答此类题关键是综合两个相似比，得出结论．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
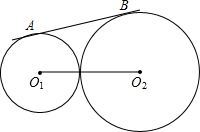如图，圆O1与圆O2相外切，两圆半径分别为2和3，则两圆公切线AB长为（ ）A、2
| ||
B、
| ||
C、2
| ||
D、2
|
（2012•烟台）如图，⊙O1，⊙O，⊙O2的半径均为2cm，⊙O3，⊙O4的半径均为1cm，⊙O与其他4个圆均相外切，图形既关于O1O2所在直线对称，又关于O3O4所在直线对称，则四边形O1O4O2O3的面积为（ ）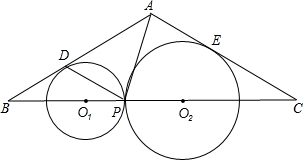
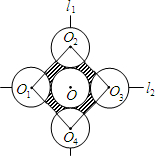如图，⊙O1，⊙O2，⊙O3，⊙O4，⊙O的半径均为2cm，⊙O与⊙O1，⊙O3相外切，⊙O与⊙O2，⊙O4相外切，并且圆心分别位于两条互相垂直的直线L1，L2上，连接O1，O2，O3，O4得四边形O1O2O3O4，则图中阴影部分的面积为（ ）平方厘米．