Question

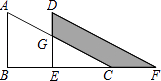
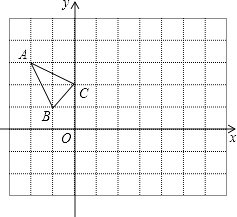
【题目】如图，已知直线y＝mx＋n与反比例函数交于A、B两点，点A在点B的左边，与x轴、y轴分别交于点C、点D，AE⊥x轴于E，BF⊥y轴于F

(1) 若m＝k，n＝0，求A，B两点的坐标(用m表示).

(2) 如图1，若A(x1，y1)、B(x2，y2)，写出y1＋y2与n的大小关系，并证明.

(3) 如图2，M、N分别为反比例函数图象上的点，AM∥BN∥x轴．若，且AM，BN之间的距离为5，则k－b＝_____________

Answer 1

【答案】（1）A(－1，m)、B(1，m)；

（2）y1＋y2＝n，证明见解析；

（3）k－b＝3

【解析】试题分析：(1)、根据反比例函数和一次函数的交点坐标的求法得出两点的坐标；(2)、首先联立方程组，得出和的值，然后得出的值；(3)、设N(，m)、B(，m)，则BN＝ 设A(，n)、M(，n)，则AM＝，根据题意得出m-n=5，然后代入得出答案.

试题解析：(1) A(－1，m)、B(1，m)

(2) 联立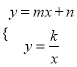，整理得mx2＋nx－k＝0 ∴x1＋x2＝，x1x2＝

∴y1＋y2＝m(x1＋x2)＋2n＝－n＋2n＝n

(3) 设N(，m)、B(，m)，则BN＝ 设A(，n)、M(，n)，则AM＝

∵ ∴ ∵AM、BN之间的距离为5 ∴m－n＝5

∴k－b＝ (m－n)＝3