题目内容
【题目】如图,在矩形纸片ABCD中,AD=5,AB=3,点E为BC上一点,沿着AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D. 
(1)当点E与点B的距离是多少时,四边形AEE'D是菱形?并说明理由;
(2)在(1)的条件下,求菱形AEE'D的两条对角线的长.
【答案】
(1)解:当BE=4时,四边形AEE'D是菱形.
理由:由△ABE平移至△DCE'的位置,可知
AD∥EE'且AD=EE'.
∴四边形AEE'D是平行四边形.
∵四边形AEE'D是菱形,
∴AE=AD=5,
∵AB=3,∠B=90°,
∴BE= ![]() =4.
=4.
∴当BE=4时,四边形AEE'D是菱形.
(2)解:∵BC=AD=5,DC=AB=3,BE=4,
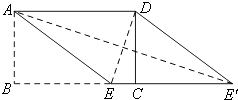
∴CE=1,BE'=9.
在Rt△DCE中, ![]() .
.
在Rt△ABE'中, ![]() .
.
【解析】(1)根据平移的性质得到AE∥DE′,AE=DE′,则由此判定四边形AEE′D是平行四边形;然后根据菱形的性质求得AE=AD=5,根据勾股定理即可求得BE;(2)根据勾股定理,可得答案.
【考点精析】利用矩形的性质和平移的性质对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等;①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.

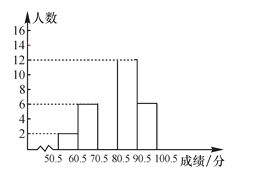
【题目】(淮安中考)某公司为了了解员工对“六五”普法知识的知晓情况,从本公司随机选取40名员工进行普法知识考查,对考查成绩进行统计(成绩均为整数,满分100分),并依据统计数据绘制了如下尚不完整的统计图表.
组别 | 分数段/分 | 频数/人数 | 频率 |
1 | 50.5~60.5 | 2 | a |
2 | 60.5~70.5 | 6 | 0.15 |
3 | 70.5~80.5 | b | c |
4 | 80.5~90.5 | 12 | 0.30 |
5 | 90.5~100.5 | 6 | 0.15 |
合计 | 40 | 1.00 |
解答下列问题:
(1)表中a=______,b=______,c=______;
(2)请补全频数分布直方图;
(3)该公司共有员工3 000人,若考查成绩80分以上(不含80分)为优秀,试估计该公司员工“六五”普法知识知晓程度达到优秀的人数.

