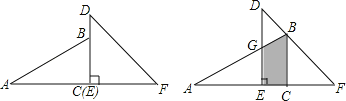题目内容
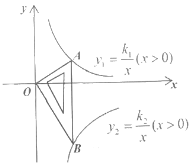
【题目】![]() 如图1,正方形
如图1,正方形![]() 和正方形,
和正方形,![]() 连接
连接![]() ,当
,当![]() 时,
时, ![]() 与
与![]() 的关系是?
的关系是?
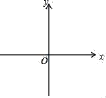
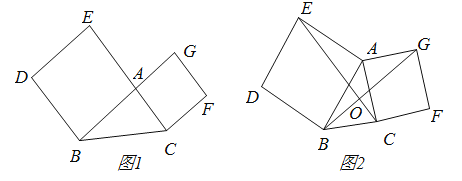
![]() 如图2,将正方形
如图2,将正方形![]() 绕点
绕点![]() 顺时针旋转,
顺时针旋转,![]()
![]() 中结论是否仍然成立?若成立,请给出证明:若不成立,请说明理由;
中结论是否仍然成立?若成立,请给出证明:若不成立,请说明理由;
![]() 已知
已知![]() ,在旋转过程中,若直线
,在旋转过程中,若直线![]() 平分
平分![]() ,请画出相应的图形,并写出其中一种情形时
,请画出相应的图形,并写出其中一种情形时![]() 长的思路.
长的思路.
【答案】(1)BG⊥CE,BG=CE;(2)(1)中结论仍然成立,理由见解析;(3)见解析
【解析】
(1)由题干提供的已知条件直接得到答案,
(2)利用正方形的性质证明△CAE≌△GAB,得到BG=CE,∠CEA=∠GBA,再利用三角形内角和可得答案,
(3)当点O在EC上时,连接BE,CG,利用已证明的结论BG⊥CE,BG=CE,结合已知条件直线![]() 平分
平分![]() 与正方形的性质,利用勾股定理列方程组即可得到答案.
与正方形的性质,利用勾股定理列方程组即可得到答案.
(1)BG⊥CE,BG=CE;
(2)(1)中结论仍然成立
证明:∵正方形ABDE和正方形ACFG,
∴AE=AB,AC=AG,∠EAB=∠CAG=90°,
∴∠EAC=∠BAG,
在△CAE和△BAG中,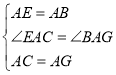 ,
,
∴△CAE≌△GAB,
∴BG=CE,∠CEA=∠GBA,
又∠1=∠2
∴∠EAB=∠EOB=90°,
∴BG⊥CE;
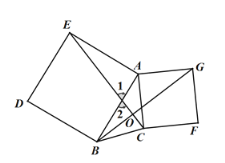
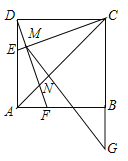
(3)①当点O在EC上时,
方法一:如图1,连接BE,CG,
设BO=GO=x,OC=y,则OE=2x-y,
利用勾股定理建立方程组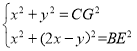 ,
,
求出x,得CE长.
(图1)
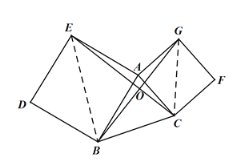
方法二:如图2,连接BE,CG,EG,作BH⊥AC于点H,
先求CG,得BC的长,再求S△ABC,
然后证明S△ABC=S△AEG,利用面积法建立方程:
![]() ,求得CE长;
,求得CE长;
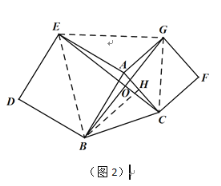
②如图3,当点O在EC延长线上时,
连接CG,作CM⊥AB于点M,GN⊥AB于点N,
由①知BC长,利用勾股定理建立方程组可求CM长
(或结合①BH长利用面积法求CM长),进而求AM长,
证△ACM≌△GAN,得AN,GN长,于是得到BN长,
再利用勾股定理求得BG长,得CE长.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案