Question

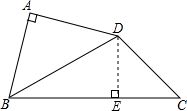
如图，四边形ABCD中，AB=AD，∠BAD=90°，∠CBD=30°，∠BCD=45°，若AB=2

2

．求四边形ABCD的面积．

Answer 1

如图，过点D作DE⊥BC于E，
∵AB=AD，∠BAD=90°，
∴AD=AB=2

2

，
BD=2

2

×

2

=4，
∵∠CBD=30°，
∴DE=

1

2

BD=

1

2

×4=2，
BE=

BD2-DE2

=

42-22

=2

3

，
∵∠BCD=45°，
∴CE=DE=2，
∴BC=BE+CE=2

3

+2，
∴四边形ABCD的面积=S_△ABD+S_△BCD=

1

2

×2

2

×2

2

+

1

2

×（2

3

+2）×2，
=4+2

3

+2，
=2

3

+6．