题目内容
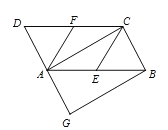
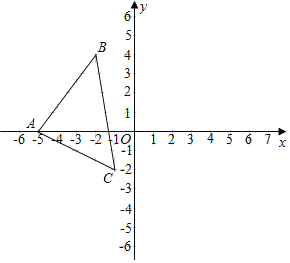
【题目】如图![]() ,在平面直角坐标系
,在平面直角坐标系 ![]() 中,已知点
中,已知点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按顺时针分别旋转
按顺时针分别旋转![]() ,
,![]() 得到
得到![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ;抛物线
;抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() .
.
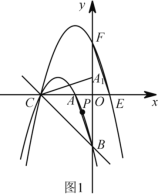
(1)求抛物线![]() 的解析式.
的解析式.
(2)如果点![]() 是直线
是直线![]() 上方抛物线
上方抛物线![]() 上的一个动点.
上的一个动点.
①若 ![]() ,求
,求![]() 点的坐标;
点的坐标;
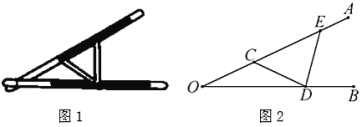
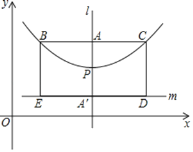
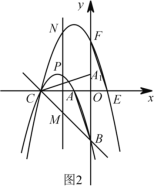
②如图![]() ,过点
,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,记
,记![]() ,求
,求![]() 与
与![]() 的函数关系式.当
的函数关系式.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)①符合条件的点
;(2)①符合条件的点![]() 的坐标为
的坐标为![]() 或
或![]() .②h=
.②h=![]() 当
当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .
.
【解析】
(1)![]() ,
,![]() 由
由![]() 旋转得到,则OC=OB=OF,OE=OA=O
旋转得到,则OC=OB=OF,OE=OA=O![]() ,所以点E的坐标为(2,0),点F坐标为(0,6),点C坐标为(-6,0),设
,所以点E的坐标为(2,0),点F坐标为(0,6),点C坐标为(-6,0),设![]() 的解析式为
的解析式为![]() ,利用待定系数法求解即可;
,利用待定系数法求解即可;
(2)①分点P在x轴上方时或在x轴下方时进行讨论求解即可得;
②过点 ![]() 作
作 ![]() 于点
于点 ![]() ,则
,则 ![]() ,结合二次函数最值问题进行求解即可得.
,结合二次函数最值问题进行求解即可得.
(1)![]() ,
,![]() 由
由![]() 旋转得到,则OC=OB=OF,OE=OA=O
旋转得到,则OC=OB=OF,OE=OA=O![]() ,所以点E的坐标为(2,0),点F坐标为(0,6),点C坐标为(-6,0),设
,所以点E的坐标为(2,0),点F坐标为(0,6),点C坐标为(-6,0),设![]() 的解析式为
的解析式为![]() ,
,
代入点坐标即可得:
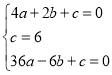
∴![]() 的解析式为
的解析式为![]() ,
,
故答案为:![]() :
:![]() ;
;
(2)①若点![]() 在
在![]() 轴的上方,且
轴的上方,且 ![]() 时,则
时,则 ![]() 与抛物线
与抛物线 ![]() 的交点即为所求的
的交点即为所求的 ![]() 点,设直线
点,设直线 ![]() 的解析式为:
的解析式为:![]() .
.
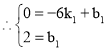
解得 
![]() 直线
直线 ![]() 的解析式为:
的解析式为:![]() ,
,
联立 
解得 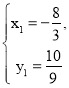 或
或 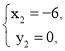
![]() .
.
若点![]() 在
在 ![]() 轴的下方,且
轴的下方,且 ![]() 时,则直线
时,则直线 ![]() 关于
关于 ![]() 轴对称的直线
轴对称的直线 ![]() 与抛物线
与抛物线 ![]() 的交点即为所求的
的交点即为所求的 ![]() 点.
点.
设直线 ![]() 的解析式为:
的解析式为:![]() .
.
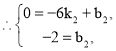
解得 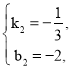
![]() 直线
直线 ![]() 的解析式为:
的解析式为:![]() .
.
联立 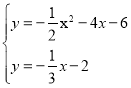 解得
解得 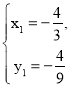 或
或 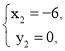
![]() ;
;
![]() 符合条件的点
符合条件的点 ![]() 的坐标为
的坐标为 ![]() 或
或 ![]() .
.
②设直线 ![]() 的解析式为:
的解析式为:![]() ,
,
![]() 解得
解得 ![]()
![]() 直线
直线 ![]() ,
,
过点 ![]() 作
作 ![]() 于点
于点 ![]() ,则
,则 ![]() ,
,
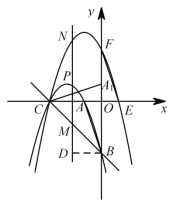
![]() ,
,
h=![]()
=![]()
=![]()
=![]()
=![]()
∴![]() ,
,
![]() ,
,
当 ![]() 时,
时,![]() 的最大值为
的最大值为 ![]() .
.
![]() ,当
,当 ![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 的取值范围是
的取值范围是 ![]() ,
,
故答案为:①符合条件的点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
②h=![]() 当
当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() .
.

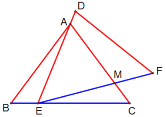
【题目】已知:点A、点B在直线![]() 的两侧.
的两侧.
(点A到直线![]() 的距离小于点B到直线
的距离小于点B到直线![]() 的距离).
的距离).
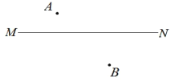
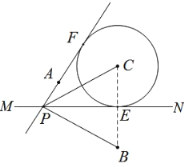
如图, (1)作点B关于直线 (2)以点C为圆心, (3)过点A作 (4)连接 |
|
根据以上作图过程及所作图形,下列四个结论中:
①![]() 是
是![]() 的切线; ②
的切线; ②![]() 平分
平分![]() ;
;
③![]() ; ④
; ④![]() .
.
所有正确结论的序号是___________________________.