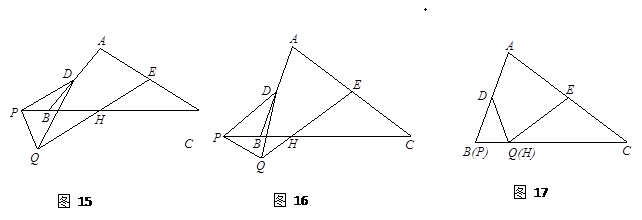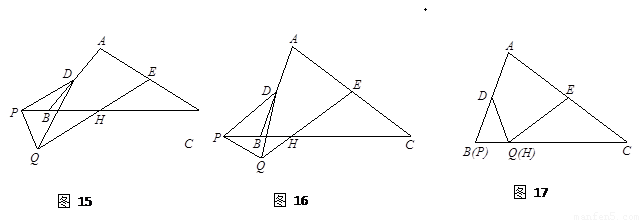题目内容
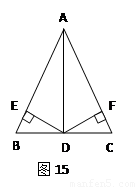
如图15,在△ABC中,BC=12,AB=10,sinB=![]() , 动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
, 动点D从点A出发,以每秒1个单位的速度沿线段AB向点B 运动,DE∥BC,交AC于点E,以DE为边,在点A的异侧作正方形DEFG.设运动时间为t,
(1)t为何值时,正方形DEFG的边GF在BC上;
(2)当GF运动到△ABC外时, EF、DG分别与BC交于点P、Q,是否存在时刻t,使得△CEP与△BDQ的面积之和等于△ABC面积的![]() ?
?
 (3)设△ABC与正方形DEFG重叠部分的面积为S,试求S的最大值.
(3)设△ABC与正方形DEFG重叠部分的面积为S,试求S的最大值.
过点A作BC边上的高AM,垂足为M,交DE于N.
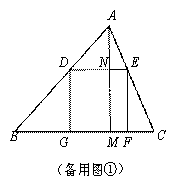 ∵AB=10,sinB=
∵AB=10,sinB=![]() ,∴AM= AB sinB= 6,
,∴AM= AB sinB= 6,
∵DE∥BC,△ADE∽△ABC,
∴![]() ,即
,即![]() ,
,
∴DE=![]() t,AN=
t,AN=![]() t,MN=6﹣
t,MN=6﹣![]() t,
t,
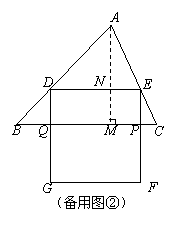
(1)当正方形DEFG的边GF在BC上时,如图①,
DE=DG=MN,即![]() t=6﹣
t=6﹣![]() t,∴t=
t,∴t=![]() ,
,
∴当t=![]() 时,正方形DEFG的边GF在BC上.……………4分
时,正方形DEFG的边GF在BC上.……………4分
(2) 当GF运动到△ABC外时,如图②,
 S△CEP+ S△BDQ=
S△CEP+ S△BDQ=![]()
=![]()
S△ABC=![]()
令![]() ,
,
解得t1=15(舍去),t2=5,
∴当t=5时,△CEP与△BDQ的面积之和等于△ABC面积的![]() .…………8分
.…………8分
(3)分两种情况:
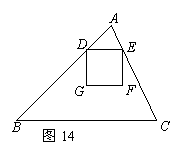 ①当正方形DEFG在△ABC的内部时,如图14,
①当正方形DEFG在△ABC的内部时,如图14,
S=DE2=(![]() t)2=
t)2=![]() t2,此时t的范围是0≤t≤
t2,此时t的范围是0≤t≤![]() ,
,
当t=![]() 时,S的最大值为16.
时,S的最大值为16.
②当正方形DEFG的一部分在△ABC的外部时,
如图②,S=DE•MN=![]() t(6﹣
t(6﹣![]() t)=﹣
t)=﹣![]() t2+
t2+![]() t,此时t
t,此时t
的范围是![]() <t≤10,
<t≤10,
∵﹣![]() <0,∴ 当t=5时,S的最大值为18,
<0,∴ 当t=5时,S的最大值为18,
∵18>16,∴S的最大值为18.

练习册系列答案
相关题目