Question

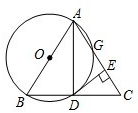如图，以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D，交AC于点G，连接AD，并过点D作DE⊥AC，垂足为E．根据以上条件写出三个正确结论（除AB=AC，AO=BO，∠ABC=∠ACB外）是：
（1）______；（2）______；（3）______．

Answer 1

解：连接OD，
∵AB是直径，
∴∠ADB=90°，
即AD⊥BC，
∵AB=AC，
∴BD=CD，
∵OA=OB，
∴OD是△ABC的中位线，
∴OD∥AC，
∵DE⊥AC，
∴DE⊥OD，
∵点D在⊙O上，
∴DE是⊙O的切线．
故答案为：（1）BD=CD，（2）DE是⊙O的切线，（3）AD⊥BC．
分析：首先连接OD，由圆周角定理可得∠ADB=90°，又由AB=AC，可得BD=CD，易证得OD是△ABC的中位线，继而证得DE是⊙O的切线．
点评：此题考查了圆周角定理、切线的判定与性质、三角形中位线的性质以及等腰三角形的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．