题目内容
完成下面的证明.
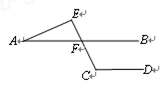
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )
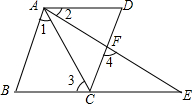
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )

完成证明见解析.
试题分析:因为AB∥CD,由此得到∠4=∠BAF,它们是同位角,由此得到根据两直线平行,同位角相等;
由∠4=∠BAF,∠3=∠4得到∠3=∠BAF的根据是等量代换;
由∠BAF=∠CAD和已知结论得到∠3=∠CAD的根据是等量代换;
由∠3=∠CAD得到AD∥BE的根据是内错角相等,两直线平行.
∵AB∥CD(已知),
∴∠4=∠BAF(两直线平行,同位角相等).
∵∠3=∠4(已知),
∴∠3=∠BAF(等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式的性质),
即∠BAF=∠CAD.
∴∠3=∠CAD(等量代换).
∴AD∥BE(内错角相等,两直线平行).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
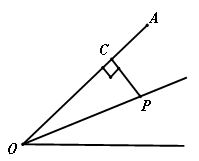
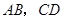 交于点
交于点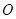 ,射线
,射线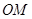 平分
平分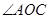 ,若
,若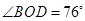 ,则
,则 .
.