题目内容
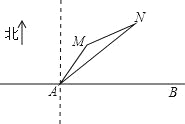
【题目】如图,公路AB为东西走向,在点A北偏东36.5°方向上,距离5千米处是村庄M;在点A北偏东53.5°方向上,距离10百米处是村庄N(参考数据;sin36.5°=0.6,cos36.5°=0.8,tan36.5°=0.75,sin23.6°=0.4,cos66.4°=0.4,tan21.8°=0.4).
(1)求M,N两村之间的距离;
(2)试问村庄N在村庄M的什么方向上?(精确到0.1度)
【答案】(1)![]() km;(2)北偏东68.2°方向上.
km;(2)北偏东68.2°方向上.
【解析】
试题分析:(1)建立直角三角形,过点M作CD∥AB,NE⊥AB,在Rt△ACM中求出CM,AC,在Rt△ANE中求出NE,AE,继而得出MD,ND的长度,在Rt△MND中利用勾股定理可得出MN的长度;(2)求出∠NMD的互余角是解题的关键,在Rt△MND中,根据tan∠NMD=![]() =
=![]() =0.4km,再根据tan21.8°=0.4,得出∠NMD=21.8°,再根据∠MND=90°﹣∠NMD,即可得出村庄N在村庄M的北偏东68.2°方向上.
=0.4km,再根据tan21.8°=0.4,得出∠NMD=21.8°,再根据∠MND=90°﹣∠NMD,即可得出村庄N在村庄M的北偏东68.2°方向上.
试题解析:(1)如图:过点M作CD∥AB,NE⊥AB:
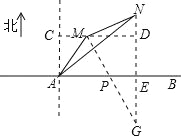 ,在Rt△ACM中,∠CAM=36.5°,AM=5km,∵sin36.5°=
,在Rt△ACM中,∠CAM=36.5°,AM=5km,∵sin36.5°=![]() =0.6,∴CM=3,AC=
=0.6,∴CM=3,AC=![]() =4km,在Rt△ANE中,∠NAE=90°﹣53.5°=36.5°,AN=10km,∵sin36.5°=
=4km,在Rt△ANE中,∠NAE=90°﹣53.5°=36.5°,AN=10km,∵sin36.5°=![]() =0.6,∴NE=6,AE=
=0.6,∴NE=6,AE=![]() =8km,∴MD=CD﹣CM=AE﹣CM=8-3=5km,ND=NE﹣DE=NE﹣AC=6-4=2km,在Rt△MND中,MN=
=8km,∴MD=CD﹣CM=AE﹣CM=8-3=5km,ND=NE﹣DE=NE﹣AC=6-4=2km,在Rt△MND中,MN=![]() =
=![]() (km);(2)在Rt△MND中,tan∠NMD=
(km);(2)在Rt△MND中,tan∠NMD=![]() =
=![]() =0.4(km),∴∠NMD=21.8°,∴∠NMD的互余角=∠MND=90°﹣21.8°=68.2°,∴村庄N在村庄M的北偏东68.2°方向上.
=0.4(km),∴∠NMD=21.8°,∴∠NMD的互余角=∠MND=90°﹣21.8°=68.2°,∴村庄N在村庄M的北偏东68.2°方向上.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案