题目内容
【题目】如图，有一块长为36米、宽为16米的长方形空地，现计划将这块空地四周和中间修等宽的道路，其余部分绿化，且绿化面积为360平方米，若设每条道路的宽为x米，则根据题意所列方程正确的是（ ）
A. 36×16－16
－36
＝360 B. 36×16－48
－2×36
＋4
＝360
C. 
D. 
【答案】C
【解析】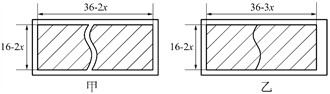
根据题意可知，这块空地除去四周的道路以外的矩形区域的长为(36-2x)米，宽为(16-2x)米. 从图甲中可以看出，这块矩形区域包含一条宽为x的道路，故此矩形区域的面积不是绿化面积，图甲中阴影部分的面积才是绿化面积. 利用平移的方法将阴影部分合并为一个矩形(如图乙所示)，则该矩形的长为(36-3x)米，宽为(16-2x)米，面积为(36-3x)(16-2x)平方米. 由于绿化面积为360平方米，所以可以列方程：(36-3x)(16-2x)=360.
故本题应选C.
练习册系列答案
相关题目
【题目】市射击队为从甲、乙两名运动员中选拔一人参加省比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
（1）根据表格中的数据，分别计算甲、乙的平均成绩；
（2）分别计算甲、乙六次测试成绩的方差；
（3）根据（1）、（2）计算的结果，你认为推荐谁参加省比赛更合适，请说明理由.