Question

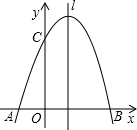
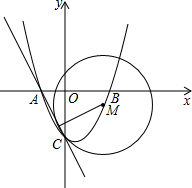
如图，过A、C两点的抛物线y=x²+bx+c上有一点M，已知A（-1，0），C（0，-2），
（1）这个抛物线的解析式为______；
（2）作⊙M与直线AC相切，切点为C，则M点的坐标为______．

Answer 1

（1）将A（-1，0），C（0，-2）的坐标代入y=x²+bx+c得

1-b+c=0 c=-2

，
解得

b=-1 c=-2

．
故此抛物线的解析式为y=x²-x-2；

（2）设直线AC的解析式为y=kx+m，将A（-1，0），C（0，-2）的坐标代入得

-k+m=0 m=-2

，
解得

k=-2 m=-2

．
故直线AC的解析式为y=-2x-2，
∵⊙M与直线AC相切，
∴与直线AC垂直的直径所在的直线为y=

1

2

x+n，
∵切点为C，
∴n=-2，
∴与直线AC垂直的直径所在的直线为y=

1

2

x-2，
设M（a，a²-a-2），
则

1

2

a-2=a²-a-2，
解得a₁=0（舍去），a₂=1.5，
∴M（1.5，-1.25）．
故答案为：y=x²-x-2，（1.5，-1.25）．