题目内容
【题目】如图1,已知矩形ABED(两组对边分别相等,四个内角都是直角),点C是边DE的中点,且AB=2AD.
(1)判断△ABC的形状,并说明理由;
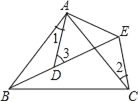
(2)保持图1中△ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
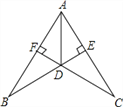
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.
 2
2
【答案】(1)△ABC是等腰直角三角形.理由见解析;
(2)DE=AD+BE.理由见解析;
(3)DE=BE-AD.理由见解析.
【解析】试题分析:(1)根据矩形的性质及勾股定理,即可判断△ABC的形状;
(2)先证明△ACD≌△CBE,然后根据线段之间的关系可得AD、BE、DE长度之间的关系;(3)通过证明△ACD≌△CBE,根据全等三角形的性质得出即可得线段AD、BE、DE长度之间的关系.
试题解析:(1)△ABC是等腰直角三角形.理由如下:
在△ADC与△BEC中,AD=BE,∠D=∠E=90°,DC=EC,
∴△ADC≌△BEC(SAS),
∴AC=BC,∠DCA=∠ECB.
∵AB=2AD=DE,DC=CE,
∴AD=DC,
∴∠DCA=45°,
∴∠ECB=45°,
∴∠ACB=180°-∠DCA-∠ECB=90°.
∴△ABC是等腰直角三角形.
(2)DE=AD+BE.理由如下:
在△ACD与△CBE中,∠ACD=∠CBE=90°-∠BCE,∠ADC=∠BEC=90°,AC=BC,
∴△ACD≌△CBE(AAS),
∴AD=CE,DC=EB.
∴DC-CE=BE-AD,
即DE=AD+BE.
(3)DE=BE-AD.理由如下:
在△ACD与△CBE中,∠ACD=∠CBE=90°-∠BCE,∠ADC=∠BEC=90°,AC=BC,
∴△ACD≌△CBE(AAS),
∴AD=CE,DC=EB.
∴DC-CE=BE-AD,
即DE=BE-AD.