题目内容
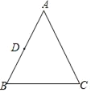
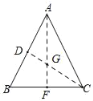
【题目】如图,在△ABC中,AB=AC,BC=4,tanB=2,以AB的中点D为圆心,r为半径作⊙D,如果点B在⊙D内,点C在⊙D外,那么r可以取( )
A.2B.3C.4D.5
【答案】B
【解析】
已知等腰三角形ABC中tanB=2,根据题意可求得△ABC中过顶点A的高AF的长度,进而求得AB的长度,以及得到BD=![]() ,;因为AF和CD均为中线,故交点为重心,通过重心到顶点的距离与重心到对边中点的距离之比为2:1,可求出CD的长度为
,;因为AF和CD均为中线,故交点为重心,通过重心到顶点的距离与重心到对边中点的距离之比为2:1,可求出CD的长度为![]() ,所以要满足B点在⊙D内,即满足r大于BD长度;要满足点C在⊙D外即r小于CD长度.
,所以要满足B点在⊙D内,即满足r大于BD长度;要满足点C在⊙D外即r小于CD长度.
如图,过点A作AF⊥BC于点F,连接CD交AF于点 G,
∵AB=AC,BC=4,
∴BF=CF=2,
∵tanB=2,
∴![]() ,即AF=4,
,即AF=4,
∴AB=![]() ,
,
∵D为AB的中点,
∴BD=![]() ,G是△ABC的重心,
,G是△ABC的重心,
∴GF=![]() AF=
AF=![]() ,
,
∴CG=![]() ,
,
∴CD=![]() CG=
CG=![]() ,
,
∵点B在⊙D内,点C在⊙D外,
∴![]() <r<
<r<![]() ,
,
故选:B.

练习册系列答案
相关题目