题目内容
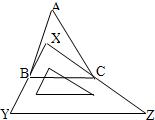6、如图，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C、△ABC中，∠A=30°，则∠ABX+∠ACX=（ ）分析：根据三角形的内角和定理，由∠A=30°，得∠ABC+∠ACB=180°-30°=150°；由∠X=90°，得∠XBC+∠XCB=180°-90°=90°，即可得到∠ABX+∠ACX．
解答：解：∵∠A=30°，
∴∠ABC+∠ACB=180°-30°=150°，
又∵∠X=90°，
∴∠XBC+∠XCB=180°-90°=90°，
∴∠ABX+∠ACX=150°-90°=60°．
故选A．
∴∠ABC+∠ACB=180°-30°=150°，
又∵∠X=90°，
∴∠XBC+∠XCB=180°-90°=90°，
∴∠ABX+∠ACX=150°-90°=60°．
故选A．
点评：本题考查了三角形的内角和定理：三角形的内角和为180°．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
5、如图，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B，C，若∠A=35°，则∠ABX+∠ACX的度数是（ ）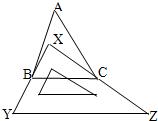
2、如图，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A=30°，则∠ABX+∠ACX=
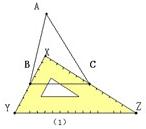26、如图，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A=40°，则∠XBA+∠XCA=
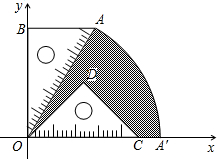ODC的斜边OC的长相等，把这两块三角板放置在如图所示的平面直角坐标系中，且AB=3，AO=6．