题目内容
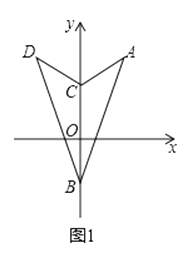
【题目】如图,已知点A(﹣m,n),B(0,m),且m、n满足 ![]() +(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.
+(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处. 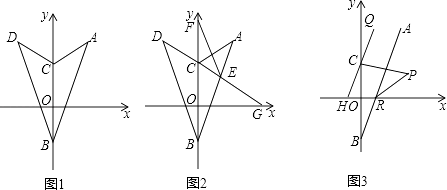
(1)写出D点坐标并求A、D两点间的距离;
(2)若EF平分∠AED,若∠ACF﹣∠AEF=20°,求∠EFB的度数;
(3)过点C作QH平行于AB交x轴于点H,点Q在HC的延长线上,AB交x轴于点R,CP、RP分别平分∠BCQ和∠ARX,当点C在y轴上运动时,∠CPR的度数是否发生变化?若不变,求其度数;若变化,求其变化范围.
【答案】
(1)解:∵ ![]() +(n﹣5)2=0,
+(n﹣5)2=0,
∴m+5=0,n﹣5=0,
∴m=﹣5,n=5,
∴A点坐标为(5,5),
∵△ABC沿y轴折叠,使点A落在点D处,
∴点D与点A关于y轴对称,
∴D点坐标为(﹣5,5);
∴AD=5﹣(﹣5)=10
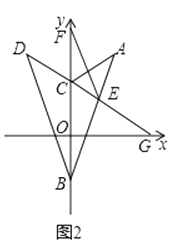
(2)解:如图2,∵△ABC沿x轴折叠,使点A落在点D处,
∴∠DCF=∠ACF,
∵∠DCF=∠EFB+∠DEF,
∴∠EFB=∠ACF﹣∠DEF,
∵EF平分∠AED,
∴∠DEF=∠AEF,
∴∠EFB=∠ACF﹣∠AEF=20°
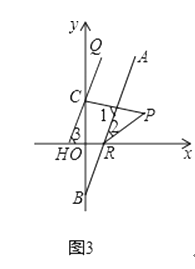
(3)解:∠CPH=45°.理由如下:
如图3,∵QH∥AB,
∴∠QCP=∠1,∠ARX=∠3,
∵CP、RP分别平分∠BCQ和∠ARX,
∴∠QCP= ![]() ∠BCQ,∠2=
∠BCQ,∠2= ![]() ∠ARX,
∠ARX,
∴∠1= ![]() ∠BCQ,∠2=
∠BCQ,∠2= ![]() ∠3,
∠3,
∵∠BCQ=90°+∠3,
∴2∠1=90°+2∠2,即∠1=45°+∠2,
∵∠1=∠CPR+∠2,
∴∠CPR=45°
【解析】(1)先由非负数的性质求出m,n的值,得到A点坐标,再根据折叠的性质得点D与点A关于y轴对称,再根据关于y轴对称的点的坐标特征得到D点坐标,然后计算点A与点D的横坐标之差即可得到A、D两点间的距离;(2)根据折叠的性质得∠DCF=∠ACF,再利用三角形外角性质得∠DCF=∠EFB+∠DEF,则∠EFB=∠ACF﹣∠DEF,又∠DEF=∠AEF,所以∠EFB=∠ACF﹣∠AEF=20°;(3)根据平行线的性质由QH∥AB得到∠QCP=∠1,∠ARX=∠3,再根据角平分线的定义得∠QCP= ![]() ∠BCQ,∠2=
∠BCQ,∠2= ![]() ∠ARX,则∠1=
∠ARX,则∠1= ![]() ∠BCQ,∠2=
∠BCQ,∠2= ![]() ∠3,接着利用三角形外角性质得∠BCQ=90°+∠3,所以2∠1=90°+2∠2,即∠1=45°+∠2,然根据∠1=∠CPR+∠2即可得到∠CPR=45°.
∠3,接着利用三角形外角性质得∠BCQ=90°+∠3,所以2∠1=90°+2∠2,即∠1=45°+∠2,然根据∠1=∠CPR+∠2即可得到∠CPR=45°.
【考点精析】通过灵活运用三角形的内角和外角和三角形的外角,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.

【题目】某学习小组13名学生的一次英语听力测试成绩分布如下表所示(满分20分):
成绩(分) | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
人数(人) | 1 | 3 | 2 | 2 | 1 | 2 | 2 |
这13名学生听力测试成绩的中位数是( )
A.16分
B.17分
C.18分
D.19分