Question

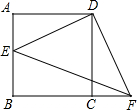如图，当△AED绕正方形ABCD的顶点D旋转到与△DCF重合时，∠DEF的度数为

45°

．

Answer 1

分析：根据正方形的性质得到DA=DC，∠ADC=90°，由于△AED绕正方形ABCD的顶点D旋转到与△DCF重合，根据旋转的性质得到旋转角等于90°，并且ED=FD，则∠EDF=90°，得到△DEF为等腰直角三角形，根据等腰直角三角形的性质即可得到∠DEF的度数．

解答：解：∵四边形ABCD为正方形，
∴DA=DC，∠ADC=90°，
∴当△AED绕正方形ABCD的顶点D旋转到与△DCF重合时，∠ADC等于旋转角，
∴旋转角等于90°，
∴∠EDF=90°，
∵△AED绕正方形ABCD的顶点D旋转到得到△DCF，
∴ED=FD，
∴△DEF为等腰直角三角形，
∴∠DEF=45°．
故答案为45°．

点评：本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了正方形和等腰直角三角形的性质．