题目内容
【题目】如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC. 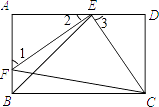
(1)求证:AE=DC;
(2)已知DC= ![]() ,求BE的长.
,求BE的长.
【答案】
(1)证明:在矩形ABCD中,∠A=∠D=90°,
∴∠1+∠2=90°,
∵EF⊥EC,
∴∠FEC=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
在△AEF和△DCE中,
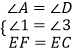 ,
,
∴△AEF≌△DCE(AAS),
∴AE=DC
(2)解:由(1)得AE=DC,
∴AE=DC= ![]() ,
,
在矩形ABCD中,AB=CD= ![]() ,
,
在R△ABE中,AB2+AE2=BE2,即( ![]() )2+(
)2+( ![]() )2=BE2,
)2=BE2,
∴BE=2
【解析】(1)根据矩形的性质和已知条件可证明△AEF≌△DCE,可证得AE=DC;(2)由(1)可知AE=DC,在Rt△ABE中由勾股定理可求得BE的长.
【考点精析】根据题目的已知条件,利用勾股定理的概念和矩形的性质的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目