题目内容
【题目】如图:CD是⊙O的直径,线段AB过圆心O,且OA=OB= ![]() ,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F.
,CD=2,连接AC、AD、BD、BC、AD、CB分别交⊙O于E、F. 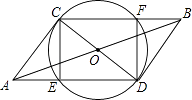
(1)问四边形CEDF是何种特殊四边形?请证明你的结论;
(2)当AC与⊙O相切时,四边形CEDF是正方形吗?请说明理由.
【答案】
(1)解:四边形CEDF是矩形.
证明:∵CD是⊙O的直径,
∴∠CFD=∠CED=90°,
∵CD⊙O的直径,
∴OC=OD,∵OA=OB,
∴四边形ADBC是平行四边形,
∴CB∥AD,
∴∠CFD+∠EDF=180°,
∴∠EDF=90°,
∴四边形CEDF是矩形
(2)解:四边形CEDF是正方形.
理由:∵AC是⊙O的切线,CD是直径,
∴∠ACD=90°,
在Rt△ACO中,OA= ![]() ,OC=
,OC= ![]() CD=1,AC2+12=5,
CD=1,AC2+12=5,
∴AC=2,
则CD=AC=2,∠CDE=45°,
∴DE=CE,
∴矩形CEDF是正方形
【解析】(1)四边形CEDF是矩形,理由是由CD是⊙O的直径,得出∠CFD=∠CED=90°,证出平行四边形ADBC,得出CB∥AD,根据平行线的性质得出∠EDF=90°,即可判断出答案;(2)在Rt△ACO中,OA= ![]() ,OC=1,根据勾股定理求出AC,推出CD=AC=2,∠CDE=45°,进一步推出DE=CE,即可推出答案.
,OC=1,根据勾股定理求出AC,推出CD=AC=2,∠CDE=45°,进一步推出DE=CE,即可推出答案.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案【题目】城区某中学为形成体育特色,落实学生每天![]() 小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
国家规定初中每班的标准人数为![]() 人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的
人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的![]() 倍少
倍少![]() 人,九年级学生人数的
人,九年级学生人数的![]() 倍刚好是七、八年级学生人数的总和.(注:
倍刚好是七、八年级学生人数的总和.(注:![]() 班表示七年级一班)
班表示七年级一班)
班级 |
|
|
|
|
|
|
|
|
和每班标准 人数的差值 |
|
|
|
|
|
|
|
|
![]() 用含
用含![]() 的式子表示该中学七年级学生总数;
的式子表示该中学七年级学生总数;
![]() 学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根
学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根![]() 元,毽球每个
元,毽球每个![]() 元,羽毛球拍每副
元,羽毛球拍每副![]() 元.请你计算当
元.请你计算当![]() 时,学校为落实
时,学校为落实![]() 小时体育锻炼时间需购买器材的费用是多少?
小时体育锻炼时间需购买器材的费用是多少?
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.