Question

【题目】如图，在长方形ABCD中，E是AD的中点，F是CE的中点．若△BDF的面积是5平方厘米，则长方形ABCD的面积是平方厘米．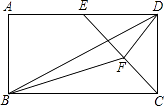

Answer 1

【答案】40
【解析】解：设这个长方形ABCD的长为a厘米，宽为b厘米．即BC=a，AB=b，则其面积为ab平方厘米． ∵E为AD的中点，F为CE的中点，
∴过F作FG⊥CD，FQ⊥BC且分别交CD于G、BC于Q，则FQ= CD= b，FG= a．
∵△BFC的面积= BCFQ= a b，
同理△FCD的面积= b a，
∴△BDF的面积=△BCD的面积﹣（△BFC的面积+△CDF的面积），
即：5= ab﹣（ ab+ ab）= ab
∴ab=40．
∴长方形ABCD的面积是40平方厘米．
所以答案是：40．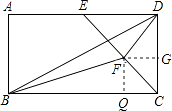

【考点精析】关于本题考查的三角形的面积，需要了解三角形的面积=1/2×底×高才能得出正确答案．