题目内容
【题目】在正方形ABCD中,CE=DF,求证:AE⊥BF. 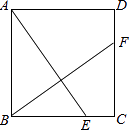
【答案】证明:∵四边形ABCD是正方形, 
∴∠ABE=∠C=90°,AB=BC,BC=CD,
∴CE=DF,
∴BE=CF,
在△ABE和△BCF中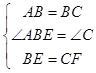
∴△ABE≌△BCF(SAS),
∴∠BAE=∠CBF,
∵∠ABE=90°,
∴∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠BOE=180°﹣90°=90°,
∴AE⊥BF.
【解析】根据正方形性质得出∠ABE=∠C=90°,AB=BC,BC=CD,求出BE=CF,根据SAS推出△ABE≌△BCF,根据全等三角形的性质得出∠BAE=∠CBF,求出∠CBF+∠AEB=90°,即可得出答案.
【考点精析】根据题目的已知条件,利用正方形的性质的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目