题目内容
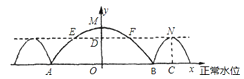
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点(点A在点B的左侧),直线l与抛物线交于A,C两点,其中点C的横坐标为2.
(1)求A,B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点(P与A,C不重合),过P点作y轴的平行线交抛物线于点E,求△ACE面积的最大值;
(3)若直线PE为抛物线的对称轴,抛物线与y轴交于点D,直线AC与y轴交于点Q,点M为直线PE上一动点,则在x轴上是否存在一点N,使四边形DMNQ的周长最小?若存在,求出这个最小值及点M,N的坐标;若不存在,请说明理由.
(4)点H是抛物线上的动点,在x轴上是否存在点F,使A、C、F、H四个点为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的F点坐标;如果不存在,请说明理由.

【答案】(1)y=﹣x﹣1;(2)△ACE的面积最大值为![]() ;(3)M(1,﹣1),N(
;(3)M(1,﹣1),N(![]() ,0);(4)满足条件的F点坐标为F1(1,0),F2(﹣3,0),F3(4+
,0);(4)满足条件的F点坐标为F1(1,0),F2(﹣3,0),F3(4+![]() ,0),F4(4﹣
,0),F4(4﹣![]() ,0).
,0).
【解析】
(1)令抛物线y=x2-2x-3=0,求出x的值,即可求A,B两点的坐标,根据两点式求出直线AC的函数表达式;
(2)设P点的横坐标为x(-1≤x≤2),求出P、E的坐标,用x表示出线段PE的长,求出PE的最大值,进而求出△ACE的面积最大值;
(3)根据D点关于PE的对称点为点C(2,-3),点Q(0,-1)点关于x轴的对称点为M(0,1),则四边形DMNQ的周长最小,求出直线CM的解析式为y=-2x+1,进而求出最小值和点M,N的坐标;
(4)结合图形,分两类进行讨论,①CF平行x轴,如图1,此时可以求出F点两个坐标;②CF不平行x轴,如题中的图2,此时可以求出F点的两个坐标.
(1)令y=0,解得![]() 或x2=3,
或x2=3,
∴A(﹣1,0),B(3,0);
将C点的横坐标x=2代入y=x2﹣2x﹣3得![]()
∴C(2,-3),
∴直线AC的函数解析式是![]()
(2)设P点的横坐标为x(﹣1≤x≤2),
则P、E的坐标分别为:P(x,﹣x﹣1),E(x,x2﹣2x﹣3),
∵P点在E点的上方,![]()
∴当![]() 时,PE的最大值
时,PE的最大值![]()
△ACE的面积最大值![]()
(3)D点关于PE的对称点为点C(2,﹣3),点Q(0,﹣1)点关于x轴的对称点为K(0,1),
连接CK交直线PE于M点,交x轴于N点,可求直线CK的解析式为![]() ,此时四边形DMNQ的周长最小,
,此时四边形DMNQ的周长最小,
最小值![]()
求得M(1,﹣1),![]()
(4)存在如图1,若AF∥CH,此时的D和H点重合,CD=2,则AF=2,
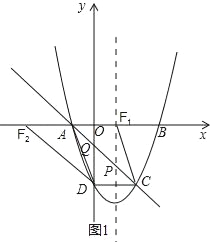
于是可得F1(1,0),F2(﹣3,0),
如图2,根据点A和F的坐标中点和点C和点H的坐标中点相同,

再根据|HA|=|CF|,
求出![]()
综上所述,满足条件的F点坐标为F1(1,0),F2(﹣3,0),![]() ,
,![]() .
.

【题目】在一次实验中,小强把一根弹簧的上端固定,在其下端悬挂物体.下面是他测得的弹簧的长度y与所挂物体的质量石的一组对应值:
所挂物体的质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度y/cm | 20 | 22 | 24 | 26 | 25 | 30 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)填空:
①当所挂的物体为3kg时,弹簧长是____.不挂重物时,弹簧长是____.
②当所挂物体的质量为8kg(在弹簧的弹性限度范围内)时,弹簧长度是___.