题目内容
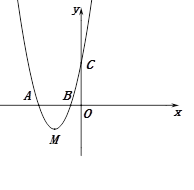
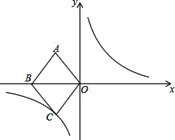
【题目】如图,在平面直角坐标系![]() 中,菱形
中,菱形![]() 的对角线
的对角线![]() 在
在![]() 轴上,若菱形
轴上,若菱形![]() 的周长为
的周长为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求该反比例函数的解析式;
(2)若点![]() 是反比例函数上的一点,且
是反比例函数上的一点,且![]() 的面积恰好等于菱形
的面积恰好等于菱形![]() 的面积,求点
的面积,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)P的坐标为
;(2)P的坐标为![]() 或
或![]() .
.
【解析】
(1)连接AC,交x轴于点D,由四边形ABCO为菱形,得到对角线互相平分且垂直,求出OD的长,由菱形四条边相等,求出OC的长,在直角三角形COD中,利用勾股定理求出CD的长,确定出点C坐标,代入反比例函数解析式求出k的值,即可确定出解析式;
(2)分两种情况考虑:若P在第一象限反比例函数图象上,连接PB,PO,求出菱形的面积即为三角形PBO面积,根据BO的长,利用三角形面积公式求出P的纵坐标,代入反比例解析式即可确定出P的坐标;若P′在第三象限反比例图象上,连接OP′,BP′,同理确定出P′坐标即可.
(1)连接AC,交x轴于点D,
∵四边形ABCO为菱形,
∴AD=DC,OD=BD,且AC⊥OB,
∵菱形的周长为20,B(6,0),
∴AB=AO=BC=OC=5,OD=BD=3,
在Rt△COD中,根据勾股定理得:![]() ,
,
∴C(3,4),
把C坐标代入反比例解析式得:k=12,
则反比例解析式为![]() ;
;

(2)分两种情况考虑:
若P在第一象限反比例函数图象上,连接PB,PO,
∵CD=AD=4,即AC=8,OB=6,
∴S菱形ABCO=![]() ,
,
![]() ,OB=6,
,OB=6,
∴![]() =8,
=8,
把y=8代入反比例函数解析式得:![]() ,
,
此时P坐标为![]() ;
;
若P′在第三象限反比例图象上,连接OP′,BP′,
同理得到![]() = -8,
= -8,
把y=8代入反比例函数解析式得:![]() ,
,
此时P′![]() ,
,
综上,P的坐标为![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目