题目内容
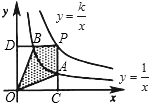 两个反比例函数y=
两个反比例函数y=| k |
| x |
| 1 |
| x |
| k |
| x |
| 1 |
| x |
| 1 |
| x |
| k |
| x |
分析:设A(x1,y1),B(x2,y2),而A、B两点都在y=
的图象上,故有x1y1=x2y2=1,而S△ODB=
×BD×OD=
x2y2=
,S△OCA=
×OC×AC=
x1y1=
,故①正确;
由A、B两点坐标可知P(x1,y2),P点在y=
的图象上,故S矩形OCPD=OC×PD=x1y2=k,根据S四边形PAOB=S矩形OCPD-S△ODB-S△OCA,计算结果,故②正确;
由已知得x1y2=k,即x1•
=k,即x1=kx2,由A、B、P三点坐标可知PA=y2-y1=
-
=
,PB=x1-x2,=(k-1)x2,故③错误;
当点A是PC的中点时,y2=2y1,代入x1y2=k中,得2x1y1=k,故k=2,代入x1=kx2中,得x1=2x2,可知④正确.
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由A、B两点坐标可知P(x1,y2),P点在y=
| k |
| x |
由已知得x1y2=k,即x1•
| 1 |
| x2 |
| 1 |
| x2 |
| 1 |
| x1 |
| k-1 |
| k x2 |
当点A是PC的中点时,y2=2y1,代入x1y2=k中,得2x1y1=k,故k=2,代入x1=kx2中,得x1=2x2,可知④正确.
解答:解:(1)设A(x1,y1),B(x2,y2),则有x1y1=x2y2=1,
∵S△ODB=
×BD×OD=
x2y2=
,S△OCA=
×OC×AC=
x1y1=
,故①正确;
(2)由已知,得P(x1,y2),
∵P点在y=
的图象上,
∴S矩形OCPD=OC×PD=x1y2=k,
∴S四边形PAOB=S矩形OCPD-S△ODB-S△OCA=k-
-
=k-1,故②正确;
(3)由已知得x1y2=k,即x1•
=k,
∴x1=kx2,
根据题意,得PA=y2-y1=
-
=
,PB=x1-x2,=(k-1)x2,故③错误;
(4)当点A是PC的中点时,y2=2y1,
代入x1y2=k中,得2x1y1=k,
∴k=2,
代入x1=kx2中,得x1=2x2,故④正确.
故本题答案为:①②④.
∵S△ODB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由已知,得P(x1,y2),
∵P点在y=
| k |
| x |
∴S矩形OCPD=OC×PD=x1y2=k,
∴S四边形PAOB=S矩形OCPD-S△ODB-S△OCA=k-
| 1 |
| 2 |
| 1 |
| 2 |
(3)由已知得x1y2=k,即x1•
| 1 |
| x2 |
∴x1=kx2,
根据题意,得PA=y2-y1=
| 1 |
| x2 |
| 1 |
| x1 |
| k-1 |
| k x2 |
(4)当点A是PC的中点时,y2=2y1,
代入x1y2=k中,得2x1y1=k,
∴k=2,
代入x1=kx2中,得x1=2x2,故④正确.
故本题答案为:①②④.
点评:本题考查了反比例函数性质的综合运用,涉及点的坐标转化,相等长度的表示方法,三角形、四边形面积的计算,充分运用双曲线上点的横坐标与纵坐标的积等于反比例系数k.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
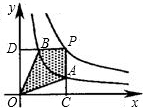 ,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( )
,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( ) 如图,两个反比例函数
如图,两个反比例函数
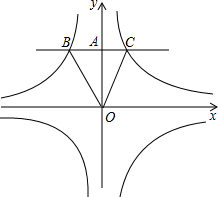 如图,已知反比例函数y=
如图,已知反比例函数y= 已知两个反比例函数
已知两个反比例函数