题目内容
已知两个反比例函数y=| 8 |
| x |
| 4 |
| x |
| 8 |
| x |
| 4 |
| x |
| 4 |
| x |
4
4
．分析：此题所求的四边形PAOB的面积可由分割法，S四边形PAOB=S□PCOD-S△DBO-S△ACO．
解答：
解：由于P点在y=
上，则S□PCOD=8，A、B两点在y=
上，
则S△DBO=S△ACO=
×4=2．
∴S四边形PAOB=S□PCOD-S△DBO-S△ACO=8-2-2=4．
∴四边形PAOB的面积为4．
故答案为：4．
解：由于P点在y=| 8 |
| x |
| 4 |
| x |
则S△DBO=S△ACO=
| 1 |
| 2 |
∴S四边形PAOB=S□PCOD-S△DBO-S△ACO=8-2-2=4．
∴四边形PAOB的面积为4．
故答案为：4．
点评：此题考查了反比例函数k的几何意义，|k|可以表示为图象上一点到两坐标轴作垂线所围成的矩形的面积．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
已知两个反比例函数y=
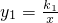和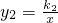
（k1＞k2＞0）在平面直角坐标系xOy第一象限内的图象如图所示，动点A在
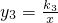，动点N在y3上，若∠AON=90°，求
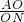的值．
已知两个反比例函数y=
（k＞0）和y=
在第一象限内的图象如图所示，点P是y=