题目内容
【题目】如图,⊙ ![]() 的圆心
的圆心 ![]() 在反比例函数
在反比例函数 ![]() 的图像上,且与
的图像上,且与 ![]() 轴、
轴、 ![]() 轴相切于点
轴相切于点 ![]() 、
、 ![]() ,一次函数
,一次函数 ![]() 的图像经过点
的图像经过点 ![]() ,且与
,且与 ![]() 轴交于点
轴交于点 ![]() ,与⊙
,与⊙ ![]() 的另一个交点为点
的另一个交点为点 ![]() .
.
(1)求 ![]() 的值及点
的值及点 ![]() 的坐标;
的坐标;
(2)求 ![]() 长及
长及 ![]() 的大小;
的大小;
(3)若将⊙ ![]() 沿
沿 ![]() 轴上下平移,使其与
轴上下平移,使其与 ![]() 轴及直线
轴及直线 ![]() 均相切,求平移的方向及平移的距离.
均相切,求平移的方向及平移的距离.
【答案】
(1)解:如图1中,连接AC、AB.

∵⊙A与x轴、y轴相切于点B、C,
∴AC⊥OC,AB⊥OB,AC=AB,四边形ABOC是正方形,设A(m,m),
∵点A在y= ![]() 上,
上,
∴m2=3,∵m>0,
∴点A坐标( ![]() ,
, ![]() ),
),
∴OC= ![]() ,
,
∴点C坐标(0, ![]() ),
),
∵一次函数y= ![]() x+b的图象经过点C,
x+b的图象经过点C,
∴b= ![]() ,
,
∴一次函数的解析式为y= ![]() ,
,
令y=0得x=-3,∴D(-3,0),b= ![]()
(2)解:如图2中,连接BC、BE,作AM⊥CE于M.
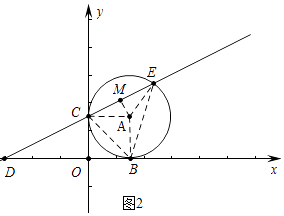
在Rt△DOC中,
∵tan∠CDO= ![]() ,
,
∴∠CDO=30°,
∵AC∥BD,
∴∠ECA=∠CDO=30°,∠CAM=60°,
∵AM⊥CE,
∴∠CAM=∠EAM=60°,
∴∠CAE=120°,
在Rt△AMC中,CM=ACcos30°= ![]() ,∴CE=2CM=3,∴∠CBE=
,∴CE=2CM=3,∴∠CBE= ![]() ∠CAE=60°
∠CAE=60°
(3)解:如图3中,
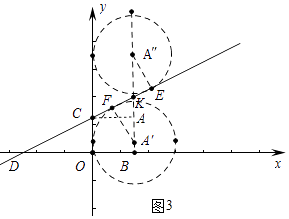
①当⊙A″与直线y= ![]() 相切于点E,AB与直线CD交于点K,
相切于点E,AB与直线CD交于点K,
∵AB∥OC,
∴∠A″KE=∠DKB=∠DCO=60°,在Rt△A″EK中,A″E= ![]() ,A″K=A″E÷cos30°=2,在Rt△CKA中,AK=CAtan30°=1,
,A″K=A″E÷cos30°=2,在Rt△CKA中,AK=CAtan30°=1,
∴AA″=A″K+AK=1+2=3,
∴⊙A向上平移3的单位⊙A与y轴及直线y= ![]() 均相切.②同理可得⊙A向下平移1个单位⊙A与y轴及直线y=
均相切.②同理可得⊙A向下平移1个单位⊙A与y轴及直线y= ![]() 均相切
均相切
【解析】(1)由⊙A与x轴、y轴相切于点B、C,得到四边形ABOC是正方形,由点A在反比例函数图像上,得到点A的坐标,求出OC的值,得到点C的坐标,由一次函数的图象经过点C![]() ,得到一次函数的解析式,得到点D的坐标,
,得到一次函数的解析式,得到点D的坐标,![]()

 阅读快车系列答案
阅读快车系列答案







