题目内容
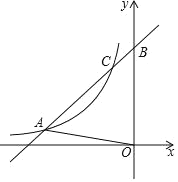
【题目】如图，矩形ABCD中，AB＝2，BC＝4，对角线AC的垂直平分线分别交AD、BC于点E、F，连接CE，则△DCE的面积为（ ）
A. 
B. 
C. 2D. 1
【答案】B
【解析】
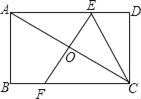
由EF垂直平分AC可得AE=CE，设CE＝x，则ED＝AD﹣AE＝4﹣x，在Rt△CDE中，利用勾股定理求出x的长，继而根据三角形的面积公式进行求解即可.
∵四边形ABCD是矩形，
∴CD＝AB＝2，AD＝BC＝4，∠D=90°，
∵EO是AC的垂直平分线，
∴AE＝CE，
设CE＝x，则ED＝AD﹣AE＝4﹣x，
在Rt△CDE中，CE2＝CD2+ED2，
即x2＝22+(4﹣x)2，
解得：x＝
，
即CE的长为，
DE＝4﹣＝
，
所以△DCE的面积＝
××2＝，
故选B．
阅读快车系列答案
【题目】为了解上一次八年级数学测验成绩情况，随机抽取了40名学生的成绩进行统计分析，这40名学生的成绩数据如下：
55 62 67 53 58 83 87 64 68 85
60 94 81 98 51 83 78 77 66 71
91 72 63 75 88 73 52 71 79 63
74 67 78 61 97 76 72 77 79 71
（1）将样本数据适当分组，制作频数分布表：
分 组 |
|
|
|
|
|
频 数 |
|
|
|
|
|
（2）根据频数分布表，绘制频数直方图：
（3）从图可以看出，这40名学生的成绩都分布在什么范围内？分数在哪个范围的人数最多？
【题目】先阅读下面的材料，再解答后面的各题：
现代社会对保密要求越来越高，密码正在成为人们生活的一部分．有一种密码的明文(真实文)按计算机键盘字母排列分解，其中Q，W，E，……，N，M这26个字母依次对应1，2，3，……，25，26这26个自然数(见下表)．
Q | W | E | R | T | Y | U | I | O | P | A | S | D |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
F | G | H | J | K | L | Z | X | C | V | B | N | M |
14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
给出一个变换公式：
将明文转成密文，如：
，即R变为L；
，即A变为S．
将密文转换成明文，如：
，即X变为P；13
3×(13－8)－1＝14，即D变为F．
(1)按上述方法将明文NET译为密文．
(2)若按上方法将明文译成的密文为DWN，请找出它的明文．