题目内容
 (2010•资阳)在军事上,常用时钟表示方位角(读数对应的时针方向),如正北为12点方向,北偏西30°为11点方向.在一次反恐演习中,甲队员在A处掩护,乙队员从A处沿12点方向以40米/分的速度前进,2分钟后到达B处.这时,甲队员发现在自己的1点方向的C处有恐怖分子,乙队员发现C处位于自己的2点方向(如图).假设距恐怖分子100米以外为安全位置.
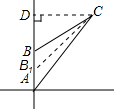
(2010•资阳)在军事上,常用时钟表示方位角(读数对应的时针方向),如正北为12点方向,北偏西30°为11点方向.在一次反恐演习中,甲队员在A处掩护,乙队员从A处沿12点方向以40米/分的速度前进,2分钟后到达B处.这时,甲队员发现在自己的1点方向的C处有恐怖分子,乙队员发现C处位于自己的2点方向(如图).假设距恐怖分子100米以外为安全位置.(1)乙队员是否处于安全位置?为什么?
(2)因情况不明,甲队员立即发出指令,要求乙队员沿原路后撤,务必于15秒内到达安全位置.为此,乙队员至少应用多快的速度撤离?(结果精确到个位.参考数据:
| 13 |
| 14 |
分析:(1)根据题意求出BC的长度,继而结合题意即可作出判断;
(2)过点C作CD⊥AB,垂足为D,在AB边上取一点B1,使CB1=100米,求出BB1的长度,即可得出撤离时需要的速度.
(2)过点C作CD⊥AB,垂足为D,在AB边上取一点B1,使CB1=100米,求出BB1的长度,即可得出撤离时需要的速度.
解答:解:(1)乙队员不安全.
易求AB=80米,
∵∠DBC=60°,∠BAC=30°,
∴∠BCA=∠BAC=30°,
∴BC=AB=80米<100米,
∴乙队员不安全.
(2)过点C作CD⊥AB,垂足为D,在AB边上取一点B1,使CB1=100米,
在Rt△CBD中,∠CBD=60°,BC=80米,则BD=40米,CD=40
米,
在Rt△CDB1中,由勾股定理知B1D=
=20
米,
则BB1=(20
-40)米,而
≈2.13秒,
依题意结果精确到个位,所以乙队员至少应以3米/秒的速度撤离.
易求AB=80米,
∵∠DBC=60°,∠BAC=30°,
∴∠BCA=∠BAC=30°,
∴BC=AB=80米<100米,
∴乙队员不安全.
(2)过点C作CD⊥AB,垂足为D,在AB边上取一点B1,使CB1=100米,

在Rt△CBD中,∠CBD=60°,BC=80米,则BD=40米,CD=40
| 3 |
在Rt△CDB1中,由勾股定理知B1D=
| B1C2-CD2 |
| 13 |
则BB1=(20
| 13 |
20
| ||
| 15 |
依题意结果精确到个位,所以乙队员至少应以3米/秒的速度撤离.
点评:本题考查了勾股定理的应用,解答本题的关键是构造直角三角形,另外要仔细审题,理解时钟所表示的方向角大小,有一定难度.

练习册系列答案
相关题目
 (2010•资阳)如图,在直角梯形ABCD中,已知AD∥BC,AB=3,AD=1,BC=6,∠A=∠B=90°.设动点P、Q、R在梯形的边上,始终构成以P为直角顶点的等腰直角三角形,且△PQR的一边与梯形ABCD的两底平行.
(2010•资阳)如图,在直角梯形ABCD中,已知AD∥BC,AB=3,AD=1,BC=6,∠A=∠B=90°.设动点P、Q、R在梯形的边上,始终构成以P为直角顶点的等腰直角三角形,且△PQR的一边与梯形ABCD的两底平行. (2010•资阳)在同一平面内,如果两个多边形(含内部)有除边界以外的公共点,则称两多边形有“公共部分”.如图,若正方形ABCD由9个边长为1的小正方形镶嵌而成,另有一个边长为1的正方形与这9个小正方形中的n个有“公共部分”,则n的最大值为( )
(2010•资阳)在同一平面内,如果两个多边形(含内部)有除边界以外的公共点,则称两多边形有“公共部分”.如图,若正方形ABCD由9个边长为1的小正方形镶嵌而成,另有一个边长为1的正方形与这9个小正方形中的n个有“公共部分”,则n的最大值为( )