题目内容
【题目】阅读下面资料:
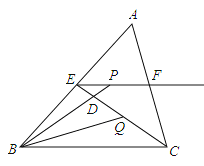
小明遇到这样一个问题:如图1,对面积为a的△ABC逐次进行以下操作:分别延长AB、BC、CA至A1、B1、C1,使得A1B2AB,B1C2BC,C1A2CA,顺次连接A1、B1、C1,得到△A1B1C1,记其面积为S1,求S1的值.

小明是这样思考和解决这个问题的:如图2,连接A1C、B1A、C1B,因为A1B2AB,B1C2BC,C1A2CA,根据等高两三角形的面积比等于底之比,所以![]()
![]() 2S△ABC2a,由此继续推理,从而解决了这个问题.
2S△ABC2a,由此继续推理,从而解决了这个问题.
(1)直接写出S1 (用含字母a的式子表示).
请参考小明同学思考问题的方法,解决下列问题:

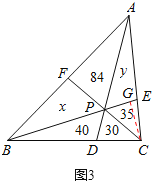
(2)如图3,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,求△ABC的面积.
(3)如图4,若点P为△ABC的边AB上的中线CF的中点,求S△APE与S△BPF的比值.
【答案】(1)19a;(2)315;(3)![]() .
.
【解析】
(1)首先根据题意,求得S△A1BC=2S△ABC,同理可求得S△A1B1C=2S△A1BC,依此得到S△A1B1C1=19S△ABC,则可求得面积S1的值;
(2)根据等高不等底的三角形的面积的比等于底边的比,求解,从而不难求得△ABC的面积;
(3)设S△BPF=m,S△APE=n,依题意,得S△APF=S△APC=m,S△BPC=S△BPF=m.得出![]() ,从而求解.
,从而求解.
解:(1)连接A1C,
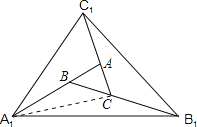
∵B1C=2BC,A1B=2AB,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理可得出:![]() ,
,
∴S1=6a+6a+6a+a=19a;
故答案为:19a;
(2)过点![]() 作
作![]() 于点
于点![]() ,
,
设![]() ,
,![]() ,
,
![]()
![]() ;
;![]() ,
,
![]()
 .
.
![]()
![]() ,即
,即![]() .
.
同理,![]() .
.
![]() .
.
![]() .①
.①
![]()
![]() ,
,![]() ,
,
![]()
![]() .②
.②
由①②,得![]() ,
,
![]() .
.
(3)设![]() ,
,![]() ,如图所示.
,如图所示.

依题意,得![]() ,
,![]() .
.
![]() .
.
![]()
![]() ,
,
![]()
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]() .
.
![]()
![]() .
.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案【题目】已知△A′B′C′是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A′B′C′ | A′(4,2) | B′(7,b) | C′(c,7) |
(1)观察表中各对应点坐标的变化,并填空:a=________,b=________,c=________;
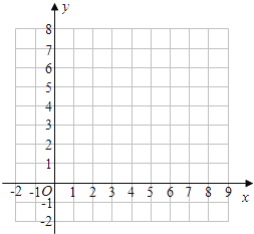
(2)在平面直角坐标系中画出△ABC及平移后的△A′B′C′;
(3)直接写出△A′B′C′的面积是________.