题目内容
已知AM是△ABC中BC边上的中线，P是△ABC的重心，过P作EF（EF∥BC），分别交AB、AC于E、F，则| BE |
| AE |
| CF |
| AF |
分析：根据平行线分线段成比例可得
=
，
=
，两式相加后再结合中位线定理即可得出答案．
| BE |
| AE |
| BG |
| AP |
| CE |
| AF |
| CK |
| AP |
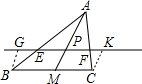
解答：解：如图分别过B、C两点作BG、CK平行于AM交直线EF于G、K，
则有
=
，
=
，
两式相加
+
=
，
又平行四边形BCKG中，PM=
（BG+CK），而由P为重心得AP=2PM，
故
+
=
=1．
故答案为：1．
则有
| BE |
| AE |
| BG |
| AP |
| CE |
| AF |
| CK |
| AP |
两式相加
| BE |
| AE |
| CF |
| AF |
| BG+CK |
| AP |
又平行四边形BCKG中，PM=
| 1 |
| 2 |
故
| BE |
| AE |
| CF |
| AF |
| 2PM |
| 2PM |
故答案为：1．
点评：本题考查平行线分线段成比例的知识，有一定难度，关键是将要求的比例关系通过平行的知识转化．
练习册系列答案
一课一练课时达标系列答案
相关题目
如图，已知在Rt△ABC中，∠BAC=90°，AB=AC，M是AC的中点，AD⊥BM于E，交BC于D点．
（2009•上海模拟）已知在正△ABC中，AB=4，点M是射线AB上的任意一点（点M与点A、B不重合），点N在边BC的延长线上，且AM=CN．连接MN，交直线AC于点D．设AM=x，CD=y．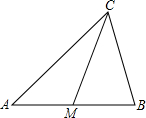
如图，已知CM是△ABC的边AB上的中线．
=________．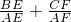