题目内容
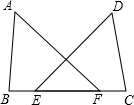 如图,点E、F在BC上,AB=DC,∠B=∠C,∠A=∠D,
如图,点E、F在BC上,AB=DC,∠B=∠C,∠A=∠D,求证:BE=CF.
分析:根据已知,利用ASA判定△ABF≌△DCE,从而得到BF=CE.则可以推出BE=CF.
解答:证明:在△ABF和△DCE中
,
∴△ABF≌△DCE.(ASA)
∴BF=CE.
∵BF-EF=CE-EF,
∴BE=CF.
|
∴△ABF≌△DCE.(ASA)
∴BF=CE.
∵BF-EF=CE-EF,
∴BE=CF.
点评:本题考查了全等三角形的判定和性质;等量减等量差相等在线段相等的证明中常常用到,是一种很常用、很重要的方法,一定要牢固掌握.

练习册系列答案
相关题目
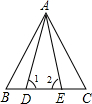 已知:如图,点D、E在BC上,BD=EC,∠1=∠2,求证:AB=AC.
已知:如图,点D、E在BC上,BD=EC,∠1=∠2,求证:AB=AC. 如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.求证:AB=DC.
如图,点E、F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.求证:AB=DC. 如图,点E、F在BC上,∠B=∠C,AB=DC,且BE=CF.
如图,点E、F在BC上,∠B=∠C,AB=DC,且BE=CF.
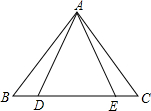 如图,点D、E在BC上,AB=AC,AD=AE.BD和CE有怎样的关系?请说明理由.
如图,点D、E在BC上,AB=AC,AD=AE.BD和CE有怎样的关系?请说明理由.