题目内容
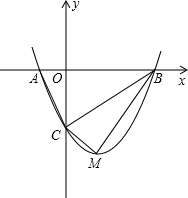 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点,点M为抛物线的顶点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点,点M为抛物线的顶点.(1)求A,B两点的坐标;
(2)是否存在以BM为斜边的Rt△BCM的抛物线?若存在,请求出抛物线的解析式;如果不存在,请说明理由;
(3)在(2)的条件下,若抛物线上有一点P,连接PC交线段BM于Q点,且S△BPQ=S△CMQ,请写出点P的坐标.
分析:(1)令y=0,解关于x的一元二次方程即可得到点A、B的坐标;
(2)根据抛物线解析式求出点C的坐标以及顶点M的坐标,然后根据勾股定理列式求出BC2,BM2,MC2,然后在Rt△BMC中,利用勾股定理列式进行计算即可求出m的值,从而得到抛物线解析式;
(3)根据m的值确定出点C、M的坐标,再利用待定系数法求一次函数解析式求出直线BC的解析式,然后根据S△BPQ=S△CMQ时则S△BPC=S△BMC,利用等底同高的三角形的面积相等可知此时MP∥BC,然后根据互相平行的两直线的解析式的k值相等以及点M的坐标求出直线MP的解析式,联立抛物线解析式求解即可得到点P的坐标.
(2)根据抛物线解析式求出点C的坐标以及顶点M的坐标,然后根据勾股定理列式求出BC2,BM2,MC2,然后在Rt△BMC中,利用勾股定理列式进行计算即可求出m的值,从而得到抛物线解析式;
(3)根据m的值确定出点C、M的坐标,再利用待定系数法求一次函数解析式求出直线BC的解析式,然后根据S△BPQ=S△CMQ时则S△BPC=S△BMC,利用等底同高的三角形的面积相等可知此时MP∥BC,然后根据互相平行的两直线的解析式的k值相等以及点M的坐标求出直线MP的解析式,联立抛物线解析式求解即可得到点P的坐标.
解答:解:(1)令y=0,则mx2-2mx-3m=0,
即x2-2x-3=0,
解得x1=-1,x2=3,
所以,点A(-1,0),B(3,0);
(2)令x=0,则y=-3m,
∴点C坐标为(0,-3m),
∵y=mx2-2mx-3m=m(x-1)2-4m,
∴抛物线的对称轴为直线x=1,顶点M坐标为(1,-4m),
∴BC2=32+(3m)2=9+9m2,BM2=(3-1)2+(4m)2=4+16m2,MC2=12+[(-3m-(-4m)]2=1+m2,
∵Rt△BCM以BM为斜边,
∴BC2+MC2=BM2,
即9+9m2+1+m2=4+16m2,
整理得,m2=1,
解得m=±1,
∵m>0,
∴m=1,
∴抛物线的解析式为y=x2-2x-3;
(3)在(2)的条件下,点C坐标为(0,-3),M(1,-4),
设直线BC的解析式为y=kx+b,
则
,
解得
,
所以直线BC的解析式为y=x-3,
∵S△BPQ=S△CMQ,
∴S△BPQ+S△BCQ=S△CMQ+S△BCQ,
即S△BPC=S△BMC,
∴点P到BC的距离等于点M到BC的距离,
∴MP∥BC,
设MP的解析式为y=x+c,
则1+c=-4,
解得c=-5,
所以,直线MP的解析式为y=x-5,
联立
,
解得
(为点M坐标),
,
所以,点P的坐标为(2,-3).
即x2-2x-3=0,
解得x1=-1,x2=3,
所以,点A(-1,0),B(3,0);
(2)令x=0,则y=-3m,
∴点C坐标为(0,-3m),
∵y=mx2-2mx-3m=m(x-1)2-4m,
∴抛物线的对称轴为直线x=1,顶点M坐标为(1,-4m),
∴BC2=32+(3m)2=9+9m2,BM2=(3-1)2+(4m)2=4+16m2,MC2=12+[(-3m-(-4m)]2=1+m2,
∵Rt△BCM以BM为斜边,
∴BC2+MC2=BM2,
即9+9m2+1+m2=4+16m2,
整理得,m2=1,

解得m=±1,
∵m>0,
∴m=1,
∴抛物线的解析式为y=x2-2x-3;
(3)在(2)的条件下,点C坐标为(0,-3),M(1,-4),
设直线BC的解析式为y=kx+b,
则
|
解得
|
所以直线BC的解析式为y=x-3,
∵S△BPQ=S△CMQ,
∴S△BPQ+S△BCQ=S△CMQ+S△BCQ,
即S△BPC=S△BMC,
∴点P到BC的距离等于点M到BC的距离,
∴MP∥BC,
设MP的解析式为y=x+c,
则1+c=-4,
解得c=-5,
所以,直线MP的解析式为y=x-5,
联立
|
解得
|
|
所以,点P的坐标为(2,-3).
点评:本题是二次函数综合题型,主要考查了求抛物线与坐标轴的交点,抛物线的顶点坐标的求解,勾股定理的应用,待定系数法求一次函数解析式,同底等高的三角形的面积相等,平行直线的解析式的k值相等,联立两函数解析式求交点坐标的问题,(3)利用过点M与BC平行的直线联立抛物线解析式求解是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
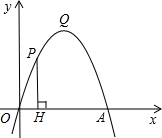 如图,抛物线y=-x2+mx过点A(4,0),O为坐标原点,Q是抛物线的顶点.
如图,抛物线y=-x2+mx过点A(4,0),O为坐标原点,Q是抛物线的顶点.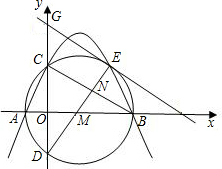 已知:如图,抛物线
已知:如图,抛物线 如图,抛物线y=
如图,抛物线y= (2010•海沧区质检)如图,抛物线y=x2+bx+c与x轴的右交点为A,顶点D在矩形OABC的边BC上,当y≤0时,x的取值范围是1≤x≤5.
(2010•海沧区质检)如图,抛物线y=x2+bx+c与x轴的右交点为A,顶点D在矩形OABC的边BC上,当y≤0时,x的取值范围是1≤x≤5. 如图,抛物线y=ax2+bx+c经过点A(5,0)、B(6,-6)和原点O,过点B的直线y=mx+n与抛物线相交于点C(2,y).过点C作平行于x轴的直线交y轴于点D,在抛物线对称轴右侧位于直线DC下方的抛物线上,任取一点P,过点P作直线PF平行于y轴,交直线DC于点E,交x轴于点F.
如图,抛物线y=ax2+bx+c经过点A(5,0)、B(6,-6)和原点O,过点B的直线y=mx+n与抛物线相交于点C(2,y).过点C作平行于x轴的直线交y轴于点D,在抛物线对称轴右侧位于直线DC下方的抛物线上,任取一点P,过点P作直线PF平行于y轴,交直线DC于点E,交x轴于点F.