题目内容
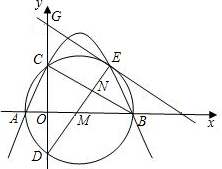 已知:如图,抛物线y=-
已知:如图,抛物线y=-
| ||
| 3 |
| 3 |
(1)求m的值和点B的坐标;
(2)过A、B、C的三点的⊙M交y轴于另一点D,设P为弧CBD上的动点P(P不与C、D重合),连接AP交y轴于点H,问是否存在一个常数k,始终满足AH•AP=k?如果存在,请求出常数k;如果不存在,请说明理由;
(3)连接DM并延长交BC于N,交⊙M于点E,过E点的⊙M的切线分别交x轴、y轴于点F、G,试探究BC与FG的位置关系,并求直线FG的解析式.
分析:(1)将A点坐标代入解析式,求出m的值,得出抛物线的具体解析式,再求出抛物线与x轴的交点坐标即为B点坐标;
(2)连接CP、AP,利用垂径定理、三角形相似(△ACH∽△APC)、勾股定理解答即可;
(3)利用圆的对称性、含30°角的直角三角形的特征、求得点F、G的坐标,就可以解决问题.
(2)连接CP、AP,利用垂径定理、三角形相似(△ACH∽△APC)、勾股定理解答即可;
(3)利用圆的对称性、含30°角的直角三角形的特征、求得点F、G的坐标,就可以解决问题.
解答:解:(1)将A(-1,0)代入解析式y=-
x2+mx+
,
解得m=
;
令y=0,即-
x2+
x+
=0,
解得x1=-1,x2=3,
因此B点坐标为(3,0);
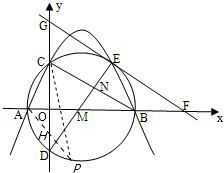 (2)如图,假设存在常数k,满足AH•AP=k
(2)如图,假设存在常数k,满足AH•AP=k
连接CP,由垂径定理可知,
∴∠P=∠ACH(或利用∠P=∠ABC=∠ACO),
又∵∠CAH=∠PAC,
∴△ACH∽△APC,
=
,
∴即AC2=AH•AP,
在Rt△AOC中,AC2=AO2+OC2=12+(
)2=4,
∴AH•AP=k=4;
(3)由A(-1,0),B(3,0)C(0,
)
根据圆的对称性,易知:⊙M半径为2,
M( 1,0)D(0,-
),
在Rt△DOM中,∠DOM=90°,OM=1,OD=
,
∴∠MDO=30°,
易得∠MFG=30°,在Rt△DGE中,∠GDE=30°,DE=4,
∴DG=
,OG=
,
∴G点的坐标为(0,
)
在Rt△GOF中∠OFG=30°,OG=
,
∴OF=5,
∴F点的坐标为(5,0)
∴直线FG的解析式为y=-
x+
.
| ||
| 3 |
| 3 |
解得m=
2
| ||
| 3 |
令y=0,即-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
解得x1=-1,x2=3,
因此B点坐标为(3,0);
 (2)如图,假设存在常数k,满足AH•AP=k
(2)如图,假设存在常数k,满足AH•AP=k连接CP,由垂径定理可知,
∴∠P=∠ACH(或利用∠P=∠ABC=∠ACO),
又∵∠CAH=∠PAC,
∴△ACH∽△APC,
| AC |
| AH |
| AP |
| AC |
∴即AC2=AH•AP,
在Rt△AOC中,AC2=AO2+OC2=12+(
| 3 |
∴AH•AP=k=4;
(3)由A(-1,0),B(3,0)C(0,
| 3 |
根据圆的对称性,易知:⊙M半径为2,
M( 1,0)D(0,-
| 3 |
在Rt△DOM中,∠DOM=90°,OM=1,OD=
| 3 |
∴∠MDO=30°,
易得∠MFG=30°,在Rt△DGE中,∠GDE=30°,DE=4,
∴DG=
| 8 |
| 3 |
| 3 |
| 5 |
| 3 |
| 3 |
∴G点的坐标为(0,
| 5 |
| 3 |
| 3 |
在Rt△GOF中∠OFG=30°,OG=
| 5 |
| 3 |
| 3 |
∴OF=5,
∴F点的坐标为(5,0)
∴直线FG的解析式为y=-
| ||
| 3 |
| 5 |
| 3 |
| 3 |
点评:此题考查勾股定理、垂径定理、相似三角形的判定与性质、圆的性质以及待定系数法求函数解析式等知识,是一道综合性很强的题目.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
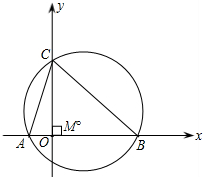 与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.
与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A( 已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0). 已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.
已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.