题目内容
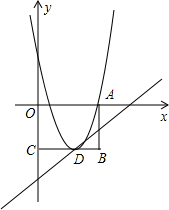 (2010•海沧区质检)如图,抛物线y=x2+bx+c与x轴的右交点为A,顶点D在矩形OABC的边BC上,当y≤0时,x的取值范围是1≤x≤5.
(2010•海沧区质检)如图,抛物线y=x2+bx+c与x轴的右交点为A,顶点D在矩形OABC的边BC上,当y≤0时,x的取值范围是1≤x≤5.(1)求b,c的值;
(2)直线y=mx+n经过抛物线的顶点D,该直线在矩形OABC内部分割出的三角形的面积记为S,求S与m的函数关系式,并写出自变量m的取值范围.
分析:(1)根据抛物线y=x2+bx+c当y≤0时,x的取值范围是1≤x≤5求得抛物线与x轴交于(1,0),(5,0),利用待定系数法求解析式即可;
(2)首先利用配方法求得D点的坐标,然后求得E点的坐标,表示出线段BD、AB、AE及BE的长,利用三角形的面积计算方法即可求得S与m之间的函数关系式.
(2)首先利用配方法求得D点的坐标,然后求得E点的坐标,表示出线段BD、AB、AE及BE的长,利用三角形的面积计算方法即可求得S与m之间的函数关系式.
解答: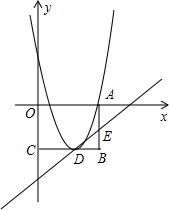 解:(1)∵抛物线y=x2+bx+c当y≤0时,x的取值范围是1≤x≤5.
解:(1)∵抛物线y=x2+bx+c当y≤0时,x的取值范围是1≤x≤5.
∴抛物线与x轴交于(1,0),(5,0)
∴
解得:b=-6 c=5;
(2)∵b=-6 c=5,
∴抛物线的解析式为y=x2-6x+5=(x-3)2-4,
∴点D的坐标为(3,-4),
∵直线y=mx+n经过抛物线的顶点D,
∴3m+n=-4,
即:n=-3m-4,
∴直线y=mx+n的解析式为y=mx-3m-4,
设直线DE与AB交于点E,
∴E点的坐标为(5,2m-4),
∴BD=2 AB=4 AE=4-2m BE=2m,
∴S=
BD•BE=±2m,
∵点E的纵坐标-5<2m-4<0
解得:-
<m<2且m≠0
∴自变量的取值范围为:-
<m<2且m≠0,
 解:(1)∵抛物线y=x2+bx+c当y≤0时,x的取值范围是1≤x≤5.
解:(1)∵抛物线y=x2+bx+c当y≤0时,x的取值范围是1≤x≤5.∴抛物线与x轴交于(1,0),(5,0)
∴
|
解得:b=-6 c=5;
(2)∵b=-6 c=5,
∴抛物线的解析式为y=x2-6x+5=(x-3)2-4,
∴点D的坐标为(3,-4),
∵直线y=mx+n经过抛物线的顶点D,
∴3m+n=-4,
即:n=-3m-4,
∴直线y=mx+n的解析式为y=mx-3m-4,
设直线DE与AB交于点E,
∴E点的坐标为(5,2m-4),
∴BD=2 AB=4 AE=4-2m BE=2m,
∴S=
| 1 |
| 2 |
∵点E的纵坐标-5<2m-4<0
解得:-
| 1 |
| 2 |
∴自变量的取值范围为:-
| 1 |
| 2 |
点评:本题考查了二次函数的综合知识,解题的关键是正确的将点的坐标转化为线段的长,体现了代数知识与几何知识的融会贯通.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
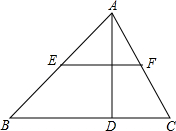 (2010•海沧区质检)已知如图,在△ABC中,AD⊥BC,中位线EF=5,AD=8,则△ABC的面积是
(2010•海沧区质检)已知如图,在△ABC中,AD⊥BC,中位线EF=5,AD=8,则△ABC的面积是 (2010•海沧区质检)如图,正方形ABCD的边长为
(2010•海沧区质检)如图,正方形ABCD的边长为