题目内容
 如图所示,在等腰梯形ABCD中,M、N分别是两底AD、BC的中点,E、F分别是BM,CM的中点.求证:四边形MENF是菱形.
如图所示,在等腰梯形ABCD中,M、N分别是两底AD、BC的中点,E、F分别是BM,CM的中点.求证:四边形MENF是菱形.
证明:∵E、F、N分别是BM,CM,BC的中点,
∴EN∥MC,FN∥BM.
∴四边形MENF是平行四边形.
∵梯形ABCD是等腰梯形,
∴AB=CD,
∴∠A=∠D.
在△ABM和△DCM中,
∵AB=DC,∠A=∠D,AM=DM,
∴△ABM≌△DCM,
∴BM=CM.
∴ME=MF,
∴平行四边形MENF是菱形.
分析:根据有一组邻边相等的平行四边形是菱形.由中点的性质,求证出四边形MENF是平行四边形.
由等腰梯形的性质知,可证△ABM≌△DCM,可证ME=MF,所以平行四边形MENF是菱形.
点评:本题利用了中点和中位线的性质,等腰梯形的性质及全等三角形的判定和性质.
∴EN∥MC,FN∥BM.
∴四边形MENF是平行四边形.
∵梯形ABCD是等腰梯形,
∴AB=CD,
∴∠A=∠D.
在△ABM和△DCM中,
∵AB=DC,∠A=∠D,AM=DM,
∴△ABM≌△DCM,
∴BM=CM.
∴ME=MF,
∴平行四边形MENF是菱形.
分析:根据有一组邻边相等的平行四边形是菱形.由中点的性质,求证出四边形MENF是平行四边形.
由等腰梯形的性质知,可证△ABM≌△DCM,可证ME=MF,所以平行四边形MENF是菱形.
点评:本题利用了中点和中位线的性质,等腰梯形的性质及全等三角形的判定和性质.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且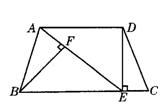 1、如图所示,在等腰梯形ABCD中,AD∥BC,DE⊥BC于点E,BF⊥AE于点F,请你添加一个条件,使△ABF≌△CDE.
1、如图所示,在等腰梯形ABCD中,AD∥BC,DE⊥BC于点E,BF⊥AE于点F,请你添加一个条件,使△ABF≌△CDE. 48、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,BF⊥AE于F,AE=BE.请你判断线段BF与图形中哪条线段相等,先写出你的猜想,再加以证明.
48、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,DE⊥BC于E,BF⊥AE于F,AE=BE.请你判断线段BF与图形中哪条线段相等,先写出你的猜想,再加以证明.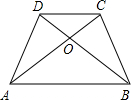 如图所示,在等腰梯形ABCD中,AB∥CD,若AB+CD=4,并且∠AOB=120°,则该等腰梯形的面积为
如图所示,在等腰梯形ABCD中,AB∥CD,若AB+CD=4,并且∠AOB=120°,则该等腰梯形的面积为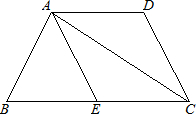 如图所示,在等腰梯形ABCD中,AD∥BC,过A作腰CD的平行线,AE∥CD,AB=AD=DC,∠B=60°
如图所示,在等腰梯形ABCD中,AD∥BC,过A作腰CD的平行线,AE∥CD,AB=AD=DC,∠B=60°