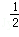Question

梯形ABCE中，AD∥BC，DC⊥BC，CE⊥AB于点E，点F在边CD上，且BE•CE=BC•CF．

（1）求证：AE•CF=BE•DF；

（2）若点E为AB中点，求证：AD•BC=2EC2-BC2．

 

 

Answer 1

(1)证明见解析；（2）证明见解析.

【解析】

试题分析：（1）求出∠B=∠DCE，证△BCE∽△CEF，推出∠BCE=∠CEF，推出EF∥BC，根据平行线分线段成比例定理得出即可．

（2）求出EF=（AD+BC），根据相似三角形的性质得出CE2=BC•EF，代入求出即可．

试题解析：（1）∵CE⊥AB，

∴∠B+∠BCE=90°，

∵DC⊥BC，

∴∠DCE+∠BCE=90°，

∴∠B=∠DCE，

∵BE×CE=BC×CF，

∴，

∴△BCE∽△CEF，

∴∠BCE=∠CEF，

∴EF∥BC，

∴，

即AE•CF=BE•DF．

（2）∵在梯形ABCD中，EF∥BC∥AD，E为AB中点，

∴F为DC的中点，

∴EF=（AD+BC），

∵△BCE∽△CEF，

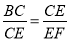∴，即CE2=BC•EF，

∴CE2=（AD+BC）•BC，

整理得：AD•BC=2EC2-BC2．

考点：相似三角形的判定与性质．