题目内容
【题目】如图,矩形OABC在平面直角坐标系中,O为坐标原点,点A(0,4),C(2,0).将矩形OABC绕点O按顺时针方向旋转135°,得到矩形EFGH(点E与O重合).
(1)若GH交y轴于点M,则∠FOM=°,OM=;
(2)将矩形EFGH沿y轴向上平移t个单位. ①直线GH与x轴交于点D,若AD∥BO,求t的值;
②若矩形EFGH与矩形OABC重叠部分的面积为S个平方单位,试求当0<t≤4 ![]() ﹣2时,S与t之间的函数关系式.
﹣2时,S与t之间的函数关系式.
【答案】
(1)45;2 ![]()
(2)解:①如图所示:连接AD,BO
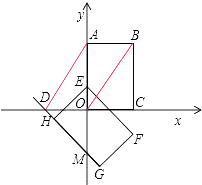
∵AD∥BO,AB∥OD,
∴四边形ADOB为平行四边形,
∴DO=AB=2,
由平移可知:∠HEM=45°,
∴∠OMD=∠ODM=45°,
∴OM=OD=2,
由平移可知:EM=2 ![]() ,
,
∴矩形EFGH平移的路程t=2 ![]() ﹣2=2(
﹣2=2( ![]() ﹣1);
﹣1);
②分三种情况考虑:
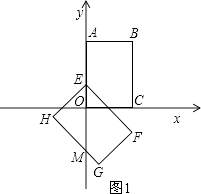
(i)如图1所示,当0<t≤2时,重叠部分为等腰直角三角形,
此时OE=t,则重叠部分面积S= ![]() t2;
t2;
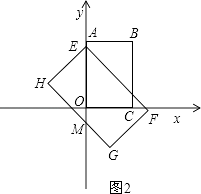
(ii)如图2所示,当2<t≤2 ![]() 时,重叠部分为直角梯形,
时,重叠部分为直角梯形,
此时S= ![]() [(t﹣2)+t]×2=2t﹣2;
[(t﹣2)+t]×2=2t﹣2;
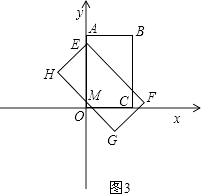
(iii)如图3所示,当2 ![]() <t≤4
<t≤4 ![]() ﹣2时,E点在A点下方,重叠部分为五边形,
﹣2时,E点在A点下方,重叠部分为五边形,
此时S=(2t﹣2)﹣ ![]() (t﹣2
(t﹣2 ![]() )2=﹣
)2=﹣ ![]() t2+2(
t2+2( ![]() +1)t﹣6.
+1)t﹣6.
综上,S= 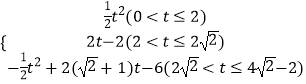 .
.
故答案为:45;2 ![]()
【解析】解:(1)如图所示: 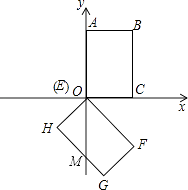
由旋转可得:∠AOF=135°,又∠AOC=90°,
∴∠COF=∠AOF﹣∠AOC=45°,又∠MOC=90°,
∴∠FOM=45°,又OF∥HG,
∴∠OMH=∠FOM=45°,又∠H=90°,
∴△OHM为等腰直角三角形,
∴OH=HM=2,
则根据勾股定理得:OM=2 ![]() ;
;
(1)由旋转可得出∠AOF=135°,再由矩形的内角为直角得到一个角为直角,利用∠AOF﹣∠AOC求出∠COF的度数,再由∠MOC为直角,由∠MOC﹣∠COF即可求出∠MOF的度数;由∠MOF的度数为45°,利用两直线平行得到一对内错角相等,可得出三角形OHM为等腰直角三角形,由OH=MH=2,利用勾股定理即可求出OM的长;(2)①如图所示,当AD与BO平行时,由AB与DO平行,利用两组对边分别平行的四边形为平行四边形得到ABOD为平行四边形,由平行四边形的对边相等得到AB=DO=2,由平移可知:∠HEM=45°,可得出∠OMD=∠ODM=45°,即三角形ODM为等腰直角三角形,得到OD=OM,由OD的长求出OM的长,由三角形HEM为等腰直角三角形,且直角边长为2,利用勾股定理求出EM的长,用EM﹣OM即可求出平移的距离,即为t的值;②分三种情况考虑:(i)如图1所示,当0<t<2时,重叠部分为等腰直角三角形,由平移的距离为t,得到等腰直角三角形直角边为t,利用三角形的面积公式即可表示出S;(ii)如图2所示,当2≤t<2 ![]() 时,重叠部分为直角梯形,表示出上底,下底及高,利用梯形的面积公式表示出S即可;(iii)图3所示,当2
时,重叠部分为直角梯形,表示出上底,下底及高,利用梯形的面积公式表示出S即可;(iii)图3所示,当2 ![]() ≤t≤4
≤t≤4 ![]() ﹣2时,重叠部分为五边形,由梯形面积﹣三角形面积,表示出S即可.
﹣2时,重叠部分为五边形,由梯形面积﹣三角形面积,表示出S即可.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案