题目内容
【题目】如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分別在矩形ABCD的边AB、CD、DA上,AH=2.
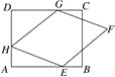
(1)已知DG=6,求AE的长;
(2)已知DG=2,求证:四边形EFGH为正方形.
【答案】(1)AE=4![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)先根据矩形的性质,利用勾股定理列出表达式:HG2=DH2+DG2,HE2=AH2+AE2,再根据菱形的性质,得到等式DH2+DG2=AH2+AE2,最后计算AE的长;
(2)先根据已知条件,用HL判定Rt△DHG≌Rt△AEH,得到菱形的一组邻边相等,进而判定该菱形为正方形.
(1)解 ∵AD=6,AH=2,
∴DH=AD-AH=4,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴在Rt△DHG中,HG2=DH2+DG2,
在Rt△AEH中,HE2=AH2+AE2,
∵四边形EFGH是菱形,
∴HG=HE,
∴DH2+DG2=AH2+AE2,
即42+62=22+AE2,
∴AE=![]() =4
=4![]() .
.
(2)证明∵AH=2,DG=2,
∴AH=DG,
∵四边形EFGH是菱形,
∴HG=HE,
在Rt△DHG和Rt△AEH中,
![]()
∴Rt△DHG≌Rt△AEH(HL),
∴∠DHG=∠AEH,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∵四边形EFGH是菱形,
∴四边形EFGH是正方形.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目