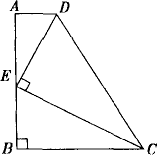
题目内容
如图，已知CB=
AB，AC=AD，AB=AE．若CB=2，求线段DE的长．
解：∵CB=AB，CB=2，
∴AB=6，
∴AC=AB-CB=6-2=4，
∵AC=AD，
∴AD=3AC=3×4=12，
∵AB=AE，
∴AE=3AB=3×6=18，
∴DE=AE-AD=18-12=6．
分析：先把CB的值代入求出AB的长，再求出AC的长，然后求出AD、AE，再根据DE=AE-AD代入数据进行计算即可得解．
点评：本题考查了两点间的距离，比较复杂，理清图中各线段之间的关系是解题的关键，要注意求出线段AC的长度．
AB，CB=2，∴AB=6，
∴AC=AB-CB=6-2=4，
∵AC=
AD，∴AD=3AC=3×4=12，
∵AB=
AE，∴AE=3AB=3×6=18，
∴DE=AE-AD=18-12=6．
分析：先把CB的值代入求出AB的长，再求出AC的长，然后求出AD、AE，再根据DE=AE-AD代入数据进行计算即可得解．
点评：本题考查了两点间的距离，比较复杂，理清图中各线段之间的关系是解题的关键，要注意求出线段AC的长度．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
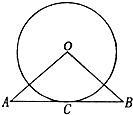20、如图，已知直线AB经过⊙O上的点C，并且OA=OB，CA=CB，那么直线AB是⊙O的切线吗？为什么？
∠ACD=∠BCE；④CB平分∠DCE，则以上结论正确的是（ ）