Question

【题目】在平面直角坐标系中，点A，B，C的坐标分别为（a，0），（2，﹣4），（c，0），且a，c满足方程为二元一次方程．

（1）求A，C的坐标．

（2）若点D为y轴正半轴上的一个动点．

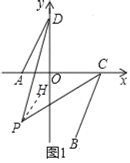
①如图1，∠AOD+∠ADO+∠DAO＝180°，当AD∥BC时，∠ADO与∠ACB的平分线交于点P，求∠P的度数；

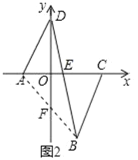
②如图2，连接BD，交x轴于点E．若S△ADE≤S△BCE成立．设动点D的坐标为（0，d），求d的取值范围．

Answer 1

【答案】（1）A（﹣2，0），C（5，0）；（2）①45°；②0＜d≤5．

【解析】

（1）根据二元一次方程的定义列式计算；

（2）①作PH∥AD，根据角平分线的定义、平行线的性质计算，得到答案；②连接AB，交y轴于F，根据点的坐标特征分别求出S△ABC、S△ABD，根据题意列出不等式，解不等式即可．

解：（1）由题意得，2a﹣4≠0，c﹣4＝1，a2﹣3＝1，

解得，a＝﹣2，c＝5，

则点A的坐标为（﹣2，0），点C的坐标为（5，0）；

（2）①作PH∥AD，

∵AD∥BC，

∴PH∥BC，

∵∠AOD＝90°，

∴∠ADO+∠OAD＝90°，

∵AD∥BC，

∴∠BCA＝∠OAD，

∴∠ADO+∠BCA＝90°，

∵∠ADO与∠BCA的平分线交于P点，

∴∠ADP＝∠ADO，∠BCP＝∠BCA，

∴∠ADP+∠BCP＝45°，

∵PH∥AD，PH∥BC，

∴∠HPD＝∠ADP，∠HPC＝∠BCP，

∴∠DPC＝∠HPD+∠HPC＝∠ADP+∠BCP＝45°；

②连接AB，交y轴于F，

∵S△ADE≤S△BCE，

∴S△ADE+S△ABE≤S△BCE+S△ABE，即S△ABD≤S△ABC，

∵A（﹣2，0），B（2，﹣4），C（5，0），

∴S△ABC＝×（2+5）×4＝14，点F的坐标为（0，﹣2），

则S△ABD＝×（2+d）×2+×（2+d）×2＝4+2d，

由题意得，4+2d≤14，

解得，d≤5，

∵点D为y轴正半轴上的一个动点，

∴0＜d≤5．