题目内容
如图,点A、B在直线MN上,AB=11cm,⊙A、⊙B的半径为1cm. ⊙A以每秒2cm的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0).
(1)当t=1时,AB= cm;当t=6时,AB= cm;
(2)问点A出发后多少秒两圆相切?
(1)当t=1时,AB= cm;当t=6时,AB= cm;
(2)问点A出发后多少秒两圆相切?

(1)9;1;(2)3秒、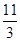 秒、11秒、13秒
秒、11秒、13秒
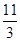 秒、11秒、13秒
秒、11秒、13秒试题分析:(1)根据点A运动的速度及AB=11cm,即可得到结果;
(2)根据两圆相切时,两圆的半径与圆心距的关系,注意有4种情况.
(1)当t=1时,AB=11-2×1=9cm;
当t=6时,AB=2×6-11=1cm;
(2)分四种情况考虑:
①当首次外切时,有
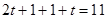 ,解得:
,解得: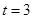 ;
;②当首次内切时,有
 ,解得:
,解得: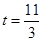 ;
;③当再次内切时,有
 ,解得:
,解得: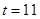 ;
;④当再次外切时,有
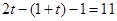 ,解得:
,解得: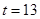 ;
;∴当点A出发后3、
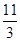 、11、13秒两圆相切.
、11、13秒两圆相切.点评:解答本题的关键是熟练掌握两圆的位置关系:外离时
 ;外切时
;外切时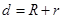 ;相交时
;相交时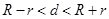 ;内切时
;内切时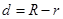 ;内含时
;内含时 .
.
练习册系列答案
相关题目
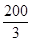 πcm2.
πcm2.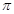 );
);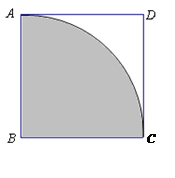
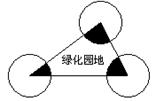
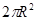
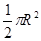
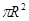


 cm
cm cm
cm cm
cm