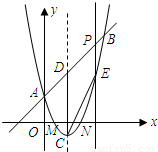
题目内容
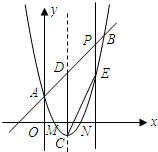
如图,⊙M与y轴的正半轴相切于点C,与x轴交于A(x1,0)、B(x2,0)两点,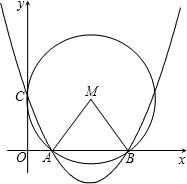 且x2>x1>0,抛物线y=
且x2>x1>0,抛物线y=| 1 | 2 |
(1)求m的值;
(2)求sin∠AMB的值;
(3)在图中的曲线上是否存在点P,使以P、A、C为顶点的三角形与△COA相似?若存在,求出所有符合条件的点P的坐标;若不存在,请说明理由.
分析:(1)过点M作x轴的垂线,垂足为点D,在直角三角形AMD中用勾股定理计算求出m的值.
(2)利用(1)中求出的m的值,得到点A,B,M的坐标,求出线段AB,MD,AM的长,然后在△ABM中,用面积法求出sin∠AMB的值.
(3)分别过A,C两点作AC的垂线,与抛物线交于点P1和点P2,因为△AOC中,OA=1,OC=2,所以当△PAC中,满足两直角边的比是1:2时,点P就存在,否则,就不存在.
(2)利用(1)中求出的m的值,得到点A,B,M的坐标,求出线段AB,MD,AM的长,然后在△ABM中,用面积法求出sin∠AMB的值.
(3)分别过A,C两点作AC的垂线,与抛物线交于点P1和点P2,因为△AOC中,OA=1,OC=2,所以当△PAC中,满足两直角边的比是1:2时,点P就存在,否则,就不存在.
解答: 解:(1)如图:过点M作MD⊥AB于点D,
解:(1)如图:过点M作MD⊥AB于点D,
当x=0时,y=m,∴C(0,m)
当y=0时,有
x2-
x+m=0
∴x1+x2=5,x1x2=2m,
AD=
AB=
(x2-x1)=
=
.
∵⊙M与y轴相切于点C,
∵AB=0B-OA=x2-x1,
∴OD=AD+OA=
AB+OA=
+x1=
(x1+x2),
∴CM=AM=OD=
(x1+x2)=
.
DM=OC=m,
在直角三角形AMD中,
AM2=AD2+MD2,
即:
=
+m2,
解得:m1=0,m2=2.
∵m>0,
∴m=2.
(2)∵m=2,
∴y=
x2-
x+2
∴C(0,2)
当y=0时,
x2-
x+2=0
解得:x1=1,x2=4,
∴A(1,0),B(4,0),
∴AB=3,AD=
,AM=
,MD=2
∵S△ABM=
AB•MD=
AM•BM•sin∠AMB,
∴
×3×2=
×
×
×sin∠AMB,
∴sin∠AMB=
.
(3)如图: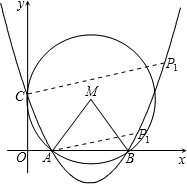
分别过点A,C作AC的垂线交抛物线于P1和P2,
∵A(1,0),C(0,2),AC=
∴AC:y=-2x+2
AP1:y=
x-
,
AP2:y=
x+2,
由
得:p1(5,2),AP1=2
,
∵
=
=
=
,
∴△P1AC∽△COA.
由
得:P2(6,5),CP2=3
,
∵
=
=
≠
,
∴△P2AC与△AOC不相似.
因此,存在点P(5,2).
 解:(1)如图:过点M作MD⊥AB于点D,
解:(1)如图:过点M作MD⊥AB于点D,当x=0时,y=m,∴C(0,m)
当y=0时,有
| 1 |
| 2 |
| 5 |
| 2 |
∴x1+x2=5,x1x2=2m,
AD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| (x2+x1)2-4x1x2 |
=
| 1 |
| 2 |
| 25-8m |
∵⊙M与y轴相切于点C,
∵AB=0B-OA=x2-x1,
∴OD=AD+OA=
| 1 |
| 2 |
| x 2-x 1 |
| 2 |
| 1 |
| 2 |
∴CM=AM=OD=
| 1 |
| 2 |
| 5 |
| 2 |
DM=OC=m,
在直角三角形AMD中,
AM2=AD2+MD2,
即:
| 25 |
| 4 |
| 25-8m |
| 4 |
解得:m1=0,m2=2.
∵m>0,
∴m=2.
(2)∵m=2,
∴y=
| 1 |
| 2 |
| 5 |
| 2 |
∴C(0,2)
当y=0时,
| 1 |
| 2 |
| 5 |
| 2 |
解得:x1=1,x2=4,
∴A(1,0),B(4,0),
∴AB=3,AD=
| 3 |
| 2 |
| 5 |
| 2 |
∵S△ABM=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
∴sin∠AMB=
| 24 |
| 25 |
(3)如图:

分别过点A,C作AC的垂线交抛物线于P1和P2,
∵A(1,0),C(0,2),AC=
| 5 |
∴AC:y=-2x+2
AP1:y=
| 1 |
| 2 |
| 1 |
| 2 |
AP2:y=
| 1 |
| 2 |
由
|
| 5 |
∵
| AC |
| AP1 |
| ||
2
|
| 1 |
| 2 |
| OA |
| OC |
∴△P1AC∽△COA.
由
|
| 5 |
∵
| AC |
| CP2 |
| ||
3
|
| 1 |
| 3 |
| 1 |
| 2 |
∴△P2AC与△AOC不相似.
因此,存在点P(5,2).
点评:本题考查的是二次函数的综合题,(1)根据二次函数的性质,利用勾股定理求出m的值.(2)用面积法求出角的正弦值.(3)根据相似三角形的性质求出点P的坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由.
作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由. (m+1).
(m+1).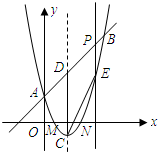 作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由.
作x轴的垂线交抛物线于点E,使四边形DCEP为平行四边形?若存在,请求出该平行四边形的面积;若不存在,说明理由.
 (m+1).
(m+1).