Question

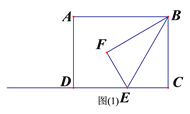
【题目】如图，小敏家厨房一墙角处有一自来水管，装修时为了美观，准备用木板从AB处将水管密封起来，互相垂直的两墙面与水管分别相切于D，E两点，经测量AD=10cm，BE=15cm， 则该自来水管的半径为（ ）cm．

A.5
B.10
C.6
D.8

Answer 1

【答案】A
【解析】解：连接OD，OE，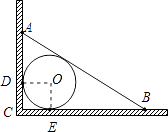
x2-25x-150=0，
（x-10）（x-15）=0，
解得：x1=10，x2=15，
∴设AD=10，BE=15，设半径为x，
∴AB=AD+BE=25，
∴（AD+x）2+（BE+x）2=AB2 ，
∴（10+x）2+（15+x）2=252 ，
解得：x=5，
故选A．
【考点精析】关于本题考查的切线长定理和根与系数的关系，需要了解从圆外一点引圆的两条切线，它们的切线长相等圆心和这一点的连线平分两条切线的夹角；一元二次方程ax2+bx+c=0（a≠0）的根由方程的系数a、b、c而定；两根之和等于方程的一次项系数除以二次项系数所得的商的相反数；两根之积等于常数项除以二次项系数所得的商才能得出正确答案．