��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A(0��4a)��B(3a��0)����AOB�������150��
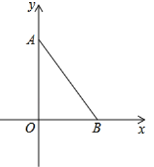
��1�����A�����ꣻ
��2����P������AB�ϵ�һ�㣬��P�ĺ�����Ϊt������PO������PBO�����ΪS�����ú���t��ʽ�ӱ�ʾS��
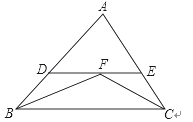
��3���ڣ�2���������£�����P�ڵ�һ�����ڣ���S��PBO��126����P��PE��AB����y���ڵ�D����x���ڵ�E����OB��OD������AE��MΪAE��һ�㣬����OM��PE�ڵ�N������EMN+��ABE��180�������N�����꣮![]()
���𰸡���1��A(0��20)����2��S��|��10t+150|����3��(��![]() ��
��![]() )
)
��������
��1���������ε������ʽ����a��ֵ���������A���ꣻ
��2������ֱ��AB����ʽ���������P���꣬�������������ʽ����S��t�Ĺ�ϵ��
��3�������PD����ʽ�������E���꣬�ɵ�EO��AO��20����AEO��45������EAO�����������ڽǺͶ�������ǵ����ʿ����DNO����FON��45�����ɵ�NF��FO���������ʽ����FO��12����������빫ʽ����⣮
�⣺��1����A��0��4a����B��3a��0����
��AO��4a��BO��3a��a��0��
�ߡ�AOB�������150��
��![]() AO��BO��150��
AO��BO��150��
��6a2��150��
��a��5������ֵ����������ȥ����
��� A��0��20����
��2����a��5��
��A��0��20����B��15��0����
��ֱ��AB����ʽΪ��y��kx+20��
��0��15k+20��
��k����![]() ��
��
��ֱ��AB����ʽΪ��y����![]() x+20��
x+20��
�ߵ�P������AB�ϵ�һ�㣬
���P��t����![]() t+20��
t+20��
��S��S��POB��![]() ��OB��|yP|
��OB��|yP|
��S��![]() ��|��
��|��![]() t+20|��|��10t+150|��
t+20|��|��10t+150|��
��3����ͼ1������O��OF��DE��
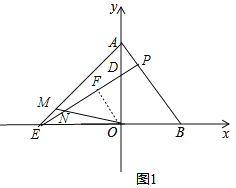
�ߵ�P�ڵ�һ�����ڣ���S��PBO��126��
��126����10t+150
��t��![]() ��
��
���P��![]() ��
��![]() ��
��
��OB��OD��15��
���D��0��15��
��ֱ��DP����ʽΪ��y��mx+15��
��![]() ��
��![]() m+15
m+15
��m��![]() ��
��
��ֱ��PD����ʽΪ��y��![]() x+15��
x+15��
�����N��x��![]() x+15��
x+15��
��ֱ��PD��x���ڵ�E��
���E����20��0����
��EO��AO��20��
���AEO��45������EAO��
�ߡ�DAP+��ADP��90������ABO+��DAP��90����
���ADP����ABO����NDO��
�ߡ�EMN+��ABE��180������EMN+��AMO��180����
���AMO����ABE����NDO��
�ߡ�AMO+��MAO+��AOM��180������NDO+��DON+��DNO��180����
���EAO����DNO��45������FO��DE��
���DNO����FON��45����
��NF��FO��
��NO��![]() FO��
FO��
�ɹ��ɶ����ɵã�DE��![]() ��
��![]() ��25��
��25��
��S��DEO��![]() DO��EO��
DO��EO��![]() ��DE��OF
��DE��OF
��OF��12��
��NO��12![]()
�ࣨx��0��2+��![]() x+15��0��2��288��
x+15��0��2��288��
��x1����![]() ��x2��
��x2��![]() ����ȥ��
����ȥ��
���N���꣨��![]() ��
��![]() ��
��

 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д� ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д� ��ٽ������½������������ϵ�д�
��ٽ������½������������ϵ�д�