题目内容
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点D在AB上,点E在BC上,且AD=BE,BD=AC.
(1)求证:CD=ED
(2)直接写出图中所有是∠ACD的2倍的角.
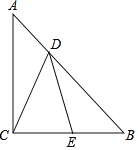
【答案】(1)见解析;(2)∠A,∠B,∠CDE是∠ACD的2倍的角
【解析】
(1)由“SAS”可证△ADC≌△BED;
(2)由全等三角形的性质可得∠ACD=∠BDE,CD=DE,由外角性质和等腰三角形的性质可求∠DCE=67.5°,即可求解.
解:(1)∵AC=BC,∠ACB=90°,
∴∠A=∠B=45°,且AD=BE,BD=AC,
∴△ADC≌△BED(SAS),
∴CD=DE.
(2)∵△ADC≌△BED,
∴∠ACD=∠BDE,CD=DE,
∵∠BDC=∠A+∠ACD=∠CDE+∠BDE,
∴∠CDE=∠A=45°,且DC=DE,
∴∠DCE=67.5°,
∴∠ACD=∠ACB﹣∠DCE=22.5°,
∵∠A=∠B=∠CDE=45°,
∴∠A,∠B,∠CDE是∠ACD的2倍的角.

练习册系列答案
相关题目